早教吧作业答案频道 -->数学-->
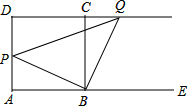
如图,点P在边长为1的正方形ABCD边AD上,连接PB.过点B作一条射线与边DC的延长线交于点Q,使得∠QBE=∠PBC,其中E是边AB延长线上的点,连接PQ.若PQ2=PB2+PD2+1,则△PAB的面积为.
题目详情
如图,点P在边长为1的正方形ABCD边AD上,连接PB.过点B作一条射线与边DC的延长线交于点Q,使得∠QBE=∠PBC,其中E是边AB延长线上的点,连接PQ.若PQ2=PB2+PD2+1,则△PAB的面积为___.

▼优质解答
答案和解析
 ∵∠QBE=∠PBC,∠QBE+∠QBC=90°,
∵∠QBE=∠PBC,∠QBE+∠QBC=90°,
∴∠PBQ=∠PBC+∠QBC=90°,
∵∠PBC+∠PBA=90°,
∴∠PBA=∠QBC,
在Rt△PAB和Rt△QCB中,
,
∴△PAB≌△QCB(ASA),
∴QC=PA,
设正方形的边长AB=a,PA=x,则QC=x,
∴DQ=DC+QC=a+x,PD=AD-PA=a-x,
在Rt△PAB中,PB2=PA2+AB2=x2+a2,
∵PQ2=PB2+PD2+1,
∴(a-x)2+(a+x)2=x2+a2+(a-x)2+1,
解得:2ax=1,
∴ax=
,
∵△PAB的面积S=
PA•PB=
ax=
×
=
.
故答案为:
.
 ∵∠QBE=∠PBC,∠QBE+∠QBC=90°,
∵∠QBE=∠PBC,∠QBE+∠QBC=90°,∴∠PBQ=∠PBC+∠QBC=90°,
∵∠PBC+∠PBA=90°,
∴∠PBA=∠QBC,
在Rt△PAB和Rt△QCB中,
|
∴△PAB≌△QCB(ASA),
∴QC=PA,
设正方形的边长AB=a,PA=x,则QC=x,
∴DQ=DC+QC=a+x,PD=AD-PA=a-x,
在Rt△PAB中,PB2=PA2+AB2=x2+a2,
∵PQ2=PB2+PD2+1,
∴(a-x)2+(a+x)2=x2+a2+(a-x)2+1,
解得:2ax=1,
∴ax=
| 1 |
| 2 |
∵△PAB的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
看了 如图,点P在边长为1的正方形...的网友还看了以下:
形成长江三角洲的主要外力作用是()A.风力沉积B.流水侵蚀C.流水沉积D.物理风形成长江三角洲的主 2020-06-19 …
对反常积分∫∞d一xxp,下列结论正确的是()A.p=1时该反常积分收敛B.p≥1时该反常积分发散 2020-07-31 …
已知a>0,b>0,则坐标平面上四个点A(a,b),B(a,-b),C.(-a,b),D(-a,- 2020-08-02 …
设A、B为n阶方阵,满足A2=B2,则必有()A.A=BB.A=-BC.|A|=|B|D.|A|2= 2020-10-31 …
设A,B均为n阶正定矩阵,则()是正定矩阵.A.A*+B*B.A*-B*C.A*B*D.k1A*+k 2020-11-02 …
读“丹霞地貌形成示意图”,回答下列各题:1.丹霞地貌的形成过程正确的是()A.c→b→d→a→f→e 2020-11-21 …
我国部分地区某等值线图,单位是卡/厘米2•年。回答问题。小题1:该等值线图反映了什么要素的分布状况? 2020-11-22 …
读下列四图,若只考虑昼夜和云量情况,下列气温排序正确的是A.a>b>c>dB.b>a>c>dC.c> 2020-12-05 …
若非零向量a和b互为相反向量,则下列说法中错误的是()A.a∥bB.a≠bC.|a|≠|b|D.b= 2020-12-07 …
如图的四幅天气图反映了一次寒潮的天气过程.结合图文材料,回答10~11题.按照此次寒潮天气发生的过程 2020-12-07 …