如图所示，轻质薄壁圆柱形容器A、B放在水平面上，容器高度都为6h，A容器底面积为2S，B容器底面积为S．A中盛有深度为3h的液体甲，B中盛有深度为4h的液体乙，在图示水平面MN处两种液体的

Question

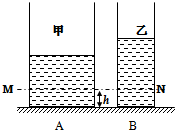
如图所示，轻质薄壁圆柱形容器A、B放在水平面上，容器高度都为6h，A容器底面积为2S，B容器底面积为S．A中盛有深度为3h的液体甲，B中盛有深度为4h的液体乙，在图示水平面MN处两种液体的压强相等．求：
①若液体乙的质量为4千克，体积为5×10^-3米³，求液体乙的密度ρ_乙．
②若液体乙的质量为4千克，求水平面对容器B的支持力F_B的大小．
③若在A容器中继续加入液体甲、在B容器中继续加入液体乙，加入的液体体积都为△V，此时容器对水平面的压强为p_A′和p_B′．请通过计算比较p_A′和p_B′的大小关系及其对应△V的取值范围．

Answer 1

①液体乙的密度：
ρ_乙=(m乙)/(V乙)=(4kg)/(5×10-3m3)=0.8×10³kg/m³；
②分析可知，轻质薄壁圆柱形容器，即不计容器重力，水平面对容器B的支持力F_B和容器B对地面的压力是一对相互作用力，大小相等，而容器B对地面的压力等于其重力，则F_B=G_乙=m_乙g=4kg×10N/kg=40N；
③A中盛有深度为3h的液体甲，B中盛有深度为4h的液体乙，在图示水平面MN处两种液体的压强相等，即p_M=p_N，
即：ρ_甲g（3h-h）=ρ_乙g（4h-h），
则ρ_甲：ρ_乙=3：2，
当p_A′=p_B′时，(F′A)/(SA)=(F′B)/(SB)，
即(ρ甲g(2S×3h+△V))/(2S)=(ρ乙g(S×4h+△V))/(S)，
所以，(3(2S×3h+△V))/(2S)=(2(S×4h+△V))/(S)，
解得，△V=2Sh，
所以，△V=2Sh时，p_A′=p_B′，
0<△V<2Sh时，p_A′>p_B′，
△V>2Sh时，B容器中液体溢出．
对应△V的取值范围为0<△V≤2Sh．
答：①液体乙的密度为0.8×10³kg/m³．
②水平面对容器B的支持力F_B的大小为40N．
③当△V=2Sh时，p_A′=p_B′，
当0<△V<2Sh时，p_A′>p_B′．