已知函数f（x）=（x2-3）ex，设关于x的方程f2(x)-mf(x)-12e2=0(m∈R)有n个不同的实数解，则n的所有可能的值为（）A.3B.1或3C.4或6D.3或4或6

Question

已知函数f（x）=（x²-3）e^x，设关于x的方程f2(x)-mf(x)-

(12)/(e2)=0(m∈R)有n个不同的实数解，则n的所有可能的值为（　　）

A. 3

B. 1或3

C. 4或6

D. 3或4或6

Answer 1

f′（x）=（x-1）（x+3）e^x，∴f（x）在（-∞，-3）和（1，+∞）上单增，（-3，1）上单减，又当x→-∞时f（x）→0，x→+∞时f（x）→+∞，故f（x）的图象大致为：

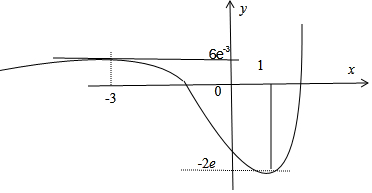
令f（x）=t，则方程t2-mt-(12)/(e2)=0必有两根t₁，t₂（t₁<t₂）且t1t2=-(12)/(e2)，
当t₁=-2e时恰有t2=6e-3，此时f（x）=t₁有1个根，f（x）=t₂有2个根；
当t₁<-2e时必有0<t2<6e-3，此时f（x）=t₁无根，f（x）=t₂有3个根；
当-2e<t₁<0时必有t2>6e-3，此时f（x）=t₁有2个根，f（x）=t₂有1个根；
综上，对任意m∈R，方程均有3个根．
故选：A．