早教吧作业答案频道 -->数学-->
如图所示点F是抛物线y2=8x的焦点,点A、B分别在抛物线y2=8x及圆(x-2)2+y2=16的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是()A、(6
题目详情
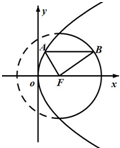 如图所示点F是抛物线y 2 =8x的焦点,点A、B分别在抛物线y 2 =8x及圆(x-2) 2 +y 2 =16的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是( )
如图所示点F是抛物线y 2 =8x的焦点,点A、B分别在抛物线y 2 =8x及圆(x-2) 2 +y 2 =16的实线部分上运动,且AB总是平行于x轴,则△FAB的周长的取值范围是( )| A、(6,10) |
| B、(8,12) |
| C、[6,8] |
| D、[8,12] |
▼优质解答
答案和解析
考点:
抛物线的简单性质
专题:
计算题 直线与圆 圆锥曲线的定义、性质与方程
分析:
由抛物线定义可得|AF|=x A +2,从而△FAB的周长=|AF|+|AB|+|BF|=x A +2+(x B -x A )+4=6+x B ,确定B点横坐标的范围,即可得到结论.
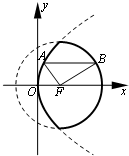 抛物线的准线l:x=-2,焦点F(2,0),
抛物线的准线l:x=-2,焦点F(2,0),
由抛物线定义可得|AF|=x A +2,
圆(x-2) 2 +y 2 =16的圆心为(2,0),半径为4,
∴△FAB的周长=|AF|+|AB|+|BF|=x A +2+(x B -x A )+4=6+x B ,
由抛物线y 2 =8x及圆(x-2) 2 +y 2 =16可得交点的横坐标为2,
∴x B ∈(2,6)
∴6+x B ∈(8,12)
故选B.
点评:
本题考查抛物线的定义,考查抛物线与圆的位置关系,确定B点横坐标的范围是关键.
考点:
抛物线的简单性质
专题:
计算题 直线与圆 圆锥曲线的定义、性质与方程
分析:
由抛物线定义可得|AF|=x A +2,从而△FAB的周长=|AF|+|AB|+|BF|=x A +2+(x B -x A )+4=6+x B ,确定B点横坐标的范围,即可得到结论.
 抛物线的准线l:x=-2,焦点F(2,0),
抛物线的准线l:x=-2,焦点F(2,0),由抛物线定义可得|AF|=x A +2,
圆(x-2) 2 +y 2 =16的圆心为(2,0),半径为4,
∴△FAB的周长=|AF|+|AB|+|BF|=x A +2+(x B -x A )+4=6+x B ,
由抛物线y 2 =8x及圆(x-2) 2 +y 2 =16可得交点的横坐标为2,
∴x B ∈(2,6)
∴6+x B ∈(8,12)
故选B.
点评:
本题考查抛物线的定义,考查抛物线与圆的位置关系,确定B点横坐标的范围是关键.
看了 如图所示点F是抛物线y2=8...的网友还看了以下:
如果一个简单的反射活动,只需感觉神经元A和运动神经元B参与完成,当A接受刺激后,兴奋的传递方向是( 2020-05-13 …
下列关于内环境稳态的说法,错误的是()A.内环境是机体进行正常生命活动和细胞代谢的场所B.维持内环 2020-05-14 …
如果一个简单的反射活动,只需感觉神经元A和运动神经元B参与完成,当A接受刺激后,兴奋的传递方向是( 2020-05-14 …
施工现场防火,下列属于一级动火的是( )。A. 现场堆有大量可燃和易燃物质的场所B. 在具有一定危 2020-05-18 …
(2009年)市场营销学中的市场概念是指( )。 A.交易发生的场所 B.买卖双方的交换关系 C.某 2020-05-30 …
市场营销学中的市场概念是指( )。A.交易发生的场所B.买卖双方的交换关系C.某种产品所有的供给方D 2020-05-30 …
人类生存对地理环境的依赖性主要表现在( ) A.地理环境是人类生存的场所 B.地理环境决定经济 2020-06-06 …
下列不属于肝细胞功能的是()A.转氨基作用发生的场所B.尿素产生的场所C.合成肌糖元的场所D.合成 2020-06-18 …
下列关于真核细胞中①~④结构与功能的叙述,正确的是()A.①是合成磷脂和氧化酒精的场所B.②是分拣 2020-06-22 …
圆柱的轴截面(经过圆柱的轴所作的截面)是边长为5cm的正方形ABCD,则圆柱侧面上从A到C的最短距 2020-06-26 …