早教吧作业答案频道 -->数学-->
如图,AB为O的直径,PD切O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.(1)求证:PB是O的切线.(2)若PB=3,DB=4,求DE的长.
题目详情
如图,AB为 O的直径,PD切 O于点C,与BA的延长线交于点D,DE⊥PO交PO延长线于点E,连接PB,∠EDB=∠EPB.
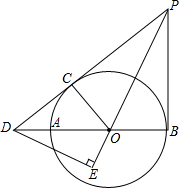
(1)求证:PB是 O的切线.
(2)若PB=3,DB=4,求DE的长.

(1)求证:PB是 O的切线.
(2)若PB=3,DB=4,求DE的长.
▼优质解答
答案和解析
(1)证明:∵在△DEO和△PBO中,∠EDB=∠EPB,∠DOE=∠POB,
∴∠OBP=∠E=90°,
∵OB为圆的半径,
∴PB为圆O的切线;
(2) 在Rt△PBD中,PB=3,DB=4,
根据勾股定理得:PD=
=5,
∵PD与PB都为圆的切线,
∴PC=PB=3,
∴DC=PD-PC=5-3=2,
在Rt△CDO中,设OC=r,则有DO=4-r,
根据勾股定理得:(4-r)2=r2+22,
解得:r=
,
∴OP=
=
,
∵∠E=∠PCO,∠CPO=∠CPO,
∴△DEP∽△OBP,
∴
=
,
∴DE=
.
∴∠OBP=∠E=90°,
∵OB为圆的半径,
∴PB为圆O的切线;
(2) 在Rt△PBD中,PB=3,DB=4,
根据勾股定理得:PD=
| 32+42 |
∵PD与PB都为圆的切线,
∴PC=PB=3,
∴DC=PD-PC=5-3=2,
在Rt△CDO中,设OC=r,则有DO=4-r,
根据勾股定理得:(4-r)2=r2+22,
解得:r=
| 3 |
| 2 |
∴OP=
| PC2+OC2 |
3
| ||
| 2 |
∵∠E=∠PCO,∠CPO=∠CPO,
∴△DEP∽△OBP,
∴
| DE |
| OB |
| DP |
| OP |
∴DE=
| 5 |
看了 如图,AB为O的直径,PD切...的网友还看了以下:
圆O的半径为5cm,点P是圆O外一点,OP=8cm,以P为圆心作圆P与圆O内切,圆P的半径是多少? 2020-05-13 …
如图,已知AB是⊙O的直径,过点A作⊙O的切线MA,P为直线MA上一动点,以点P为圆心,PA为半径 2020-05-17 …
如图,P为⊙O外一点,PA切⊙O于点A.过点P的任一直线交⊙O于B、C两点,连接AB、AC,连接P 2020-06-13 …
如图:已知菱形ABCD中,对角线AC和BD相交于点O,AC=8,BD=6,动点P在边AB上运动,以 2020-07-06 …
如图,在Rt△ABC中∠ACB=90°,AC=6,AB=10,CD是斜边AB上的中线,以AC为直径 2020-07-21 …
(2002•东城区)已知如图P是⊙O直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF⊥ 2020-07-21 …
如图,∠BAC=60°,半径长为1的圆O与∠BAC的两边相切,P为圆O上一动点,以P为圆心,PA长 2020-07-31 …
如图,A是半径为5的圆O上的一个定点,单位向量AB在A点处与圆O相切,点P是圆O上的一个动点,且点 2020-07-31 …
如图所示.⊙O的半径为5厘米.点P是⊙O外一点,OP=8厘米.求:(1)以P为圆心作⊙P与⊙O外切, 2020-11-26 …
如图,圆O的半径为2,P是圆O的直径AB延长线上的一点,BP=1,割线PCD交圆O于C、D两点,过P 2020-12-05 …