早教吧作业答案频道 -->数学-->
设正整数n≥2,对2×n格点链中的2n个结点用红(R)、黄(Y)、蓝(B)三种颜色染色,左右端点中的三个结点己经染好色,如图所示.若对剩余的2n-3个结点,要求每个结点恰染-种颜色,相邻
题目详情
设正整数n≥2,对2×n格点链中的2n个结点用红(R)、黄(Y)、蓝(B)三种颜色染色,左右端点中的三个结点己经染好色,如图所示.若对剩余的2n-3个结点,要求每个结点恰染-种颜色,相邻结点异色,求不同的染色方法数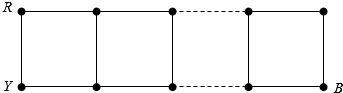

▼优质解答
答案和解析
2×n格点链中的2n个结点用红(R)、黄(Y)、蓝(B)三种颜色染色,其中最左端点染成红色与黄色,设右端点染色为P,Q,如图所示:
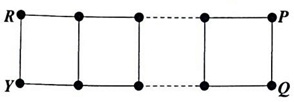
记P=R(或Y),Q=B时的着色数目为an,
记P=B,Q=R(或Y)时的着色数目为bn,
记P=R,Q=Y或者P=Y,Q=R时的着色数目为cn,
我们注意到:(1)若右端没有约束时,每增加一个格子都有3种不同的着色方法,则an+bn+cn=3n-1,
(2)由对称性,即将图形山下翻转,并且颜色R与Y互换,可知an=bn,
(3)考虑相互的递推特征,如图:则an=2bn-1+cn-1,

所以,
,n∈N*
这样an=2bn-1+cn-1=an-1+bn-1+cn-1=3n-2,
即为问题所求的不同的染色方法数.

记P=R(或Y),Q=B时的着色数目为an,
记P=B,Q=R(或Y)时的着色数目为bn,
记P=R,Q=Y或者P=Y,Q=R时的着色数目为cn,
我们注意到:(1)若右端没有约束时,每增加一个格子都有3种不同的着色方法,则an+bn+cn=3n-1,
(2)由对称性,即将图形山下翻转,并且颜色R与Y互换,可知an=bn,
(3)考虑相互的递推特征,如图:则an=2bn-1+cn-1,

所以,
|
这样an=2bn-1+cn-1=an-1+bn-1+cn-1=3n-2,
即为问题所求的不同的染色方法数.
看了 设正整数n≥2,对2×n格点...的网友还看了以下:
关于生物必修三中P37页细胞免疫示意图的一些问题原先宿主细胞上有个绿色点,效应T细胞与它密切接触后便 2020-03-31 …
在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列如图,在平面直角坐标系中,有若干个整 2020-05-16 …
已知,A、B、C、D、E是反比例函数y=16x(x>0)图象上五个整数点(横,纵坐标均为整数),分 2020-06-27 …
数轴上表示整数的点为整点,某数轴上的单位长度是1cm,若在这个数轴上随意放上一根长为5cm的木棒该 2020-06-29 …
数轴上标出若干个整数点,每相邻两点相距一个单位,点M,N,P,Q分别表示整数m,n,p,q,且q- 2020-07-11 …
(2014•邯郸二模)如图,在数轴上有A、B、C、D四个整数点(即各点均表示整数),且2AB=BC 2020-07-20 …
已知ABCDE是反比例函数y=16/x(x>0)图像上五个整数点(横、纵坐标均为整数),分别以这些 2020-07-29 …
如图,小米同学家位于A点,学校位于B点,建立数轴,若数轴上的一个整数点到小米家与学校的距离之和为7 2020-08-01 …
在数轴上有A、B、C、D、E、F五个整数点(几个点均表示证书),且AB=2BC=3CD=4DE,若A 2020-12-04 …
在已知的坐标系中,任意给出三个不在同一直线上的三个整数点,就构成定点坐标为整数的三角形,这样的三角形 2020-12-25 …