早教吧作业答案频道 -->数学-->
如图,已知关于x的二次函数y=x2+mx的图象经过原点O,并且与x轴交于点A,对称轴为直线x=1.(1)常数m=,点A的坐标为;(2)若关于x的一元二次方程x2+mx=n(n为常数)有两个不相等的实
题目详情
如图,已知关于x的二次函数y=x2+mx的图象经过原点O,并且与x轴交于点A,对称轴为直线x=1.
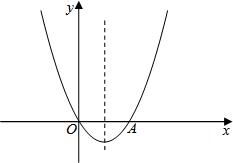
(1)常数m=___,点A的坐标为___;
(2)若关于x的一元二次方程x2+mx=n(n为常数)有两个不相等的实数根,求n的取值范围;
(3)若关于x的一元二次方程x2+mx-k=0(k为常数)在-2<x<3的范围内有解,求k的取值范围.

(1)常数m=___,点A的坐标为___;
(2)若关于x的一元二次方程x2+mx=n(n为常数)有两个不相等的实数根,求n的取值范围;
(3)若关于x的一元二次方程x2+mx-k=0(k为常数)在-2<x<3的范围内有解,求k的取值范围.
▼优质解答
答案和解析
(1)∵对称轴为直线x=1,
∴-
=1,m=-2,
则二次函数解析式为y=x2-2x,
x2-2x=0,x=0或2,
∴点A的坐标为 (2,0),
∴常数m=-2,点A的坐标为 (2,0);
(2)∵一元二次方程x2-2x=n有两个不相等的实数根,
∴△=4+4n>0,
n>-1
(3)一元二次方程x2-2x-k=0有解,
则△=4+4k≥0,
k≥-1,
方程的解为:x=1±
,
∵方程在-2<x<3的范围内有解,
1-
>-2,k<8,
1+
<3,k<3,
∴-1≤k<8.
∴-
| m |
| 2 |
则二次函数解析式为y=x2-2x,
x2-2x=0,x=0或2,
∴点A的坐标为 (2,0),
∴常数m=-2,点A的坐标为 (2,0);
(2)∵一元二次方程x2-2x=n有两个不相等的实数根,
∴△=4+4n>0,
n>-1
(3)一元二次方程x2-2x-k=0有解,
则△=4+4k≥0,
k≥-1,
方程的解为:x=1±
| 1+k |
∵方程在-2<x<3的范围内有解,
1-
| 1+k |
1+
| 1+k |
∴-1≤k<8.
看了 如图,已知关于x的二次函数y...的网友还看了以下:
高一数学指数,对数函数!要详细过程!请指教!一.求下列函数的定义域.1.y=根号下的1-3^x2. 2020-04-27 …
求1+2+2的2次方+2^3……+2^2012的值,可令S=1+2+2^2+2^3+…+2^201 2020-05-15 …
二次函数P在边长为2的正方形ABCD移动,路程为X, 三角形PAC面积y求解析式在边长为2的正方形 2020-05-17 …
预习数学的时产生了疑惑.2的负2次方等于多少?(一下个人理解)2³=2×2×2=8(表示为3个2相 2020-05-21 …
y={1+2(的2次方)}分之{1—2(的2次方)},定义域怎么求?最好写过程y={1+2(的x次 2020-05-23 …
为了求1+2+2的2次方+2^3……+2^2012的值,可令S=1+2+2^2+2^3+…+2^2 2020-06-17 …
外贸函电的帮忙翻译!我自己会一点,不知道对不对!谢谢了~~急!我们是从渥太华的大使馆的商务处获知你 2020-06-29 …
2的1次方等于2,2的2次方等于4,2的3次方等于8,2的4次方等于16,2的5次方等于32,2的 2020-07-04 …
求1+2+2^2+2^3+2^4+…+2^2014的值.设S=1+2+2^2+2^3+2^4+…+ 2020-07-09 …
2的n次方求2的N次方的位数的公式如2^1=2(1)2^2=4(1)2^3=8(1)2^4=16( 2020-07-19 …