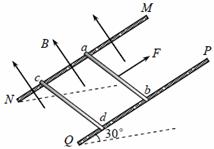
如图所示，两根足够长的光滑金属导轨MN、PQ间距为l=0.5m，其电阻不计，两导轨及其构成的平面均与水平面成30°角。完全相同的两金属棒ab、cd分别垂直导

Question

如图所示，两根足够长的光滑金属导轨 MN 、 PQ 间距为 l =0.5m ，其电阻不计，两导轨及其构成的平面均与水平面成 30 °角。完全相同的两金属棒 ab 、 cd 分别垂直导轨放置，每棒两端都与导轨始终有良好接触，已知两棒的质量均为 0.02kg ，电阻均为 R =0.1 Ω ，整个装置处在垂直于导轨平面向上的匀强磁场中，磁感应强度为 B =0.2T ，棒 ab 在平行于导轨向上的力 F 作用下，沿导轨向上匀速运动，而棒 cd 恰好能保持静止。取 g =10m/s ² ，问：

（ 1 ）通过 cd 棒的电流 I 是多少，方向如何？

（ 2 ）棒 ab 受到的力 F 多大？

（ 3 ）棒 cd 每产生 Q =0.1J 的热量，力 F 做的功 W 是多少？

Answer 1

（ 1 ）棒 cd 受到的安培力                                                                                                  ①

棒 cd 在共点力作用下平衡，则                                                                      ②

由①②式代入数据解得 I =1A ，方向由右手定则可知由 d 到 c 。

（ 2 ）棒 ab 与棒 cd 受到的安培力大小相等 F _ab = F _cd

对棒 ab 由共点力平衡有                                                                           ③

代入数据解得 F =0.2N                                                                                                             ④

（ 3 ）设在时间 t 内棒 cd 产生 Q =0.1J 热量，由焦耳定律可知                                             ⑤

设 ab 棒匀速运动的速度大小为 v ，则产生的感应电动势 E=Blv                                              ⑥

由闭合电路欧姆定律知                                                                                              ⑦

由运动学公式知，在时间 t 内，棒 ab 沿导轨的位移 x = vt                                                         ⑧

力 F 做的功 W = Fx                                                                                                                  ⑨

综合上述各式，代入数据解得 W =0.4J