早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE(1)求∠ECD的度数;(2)若∠ACB为α,则∠ECD的度数能否用含α的式子来表示?并证明你的结论.
题目详情
如图,在△ABC中,∠ACB=90°,点D,E在AB上,且AF垂直平分CD,BG垂直平分CE
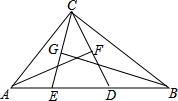
(1)求∠ECD的度数;
(2)若∠ACB为α,则∠ECD的度数能否用含α的式子来表示?并证明你的结论.

(1)求∠ECD的度数;
(2)若∠ACB为α,则∠ECD的度数能否用含α的式子来表示?并证明你的结论.
▼优质解答
答案和解析
(1)设∠ADC=x,∠BEC=y.
∵AF垂直平分CD,
∴AC=AD,
∴∠ADC=∠ACD=x,
同理∠BEC=∠BCE=y.
在△ACD中,∵∠ADC+∠ACD+∠CAD=180°,
∴2x+∠CAD=180°①,
同理,2y+∠CBE=180°②,
①+②,得2x+2y+∠CAD+∠CBE=360°③,
∵∠CAD+∠CBE+∠ACB=180°,∠ACB=90°,
∴∠CAD+∠CBE=90°④,
④代入③,得2x+2y+90°=360°,
∴x+y=135°,
∴∠ECD=180°-(x+y)=45°;
(2)由(1)可得2x+2y+∠CAD+∠CBE=360°,
∵∠CAD+∠CBE=180°-∠ACB=180°-α,
∴2x+2y+180°-α=360°,
∴x+y=90°+
α,
∴∠ECD=180°-(x+y)=180°-(90°+
α)=90°-
α.
∵AF垂直平分CD,
∴AC=AD,
∴∠ADC=∠ACD=x,
同理∠BEC=∠BCE=y.
在△ACD中,∵∠ADC+∠ACD+∠CAD=180°,
∴2x+∠CAD=180°①,
同理,2y+∠CBE=180°②,
①+②,得2x+2y+∠CAD+∠CBE=360°③,
∵∠CAD+∠CBE+∠ACB=180°,∠ACB=90°,
∴∠CAD+∠CBE=90°④,
④代入③,得2x+2y+90°=360°,
∴x+y=135°,
∴∠ECD=180°-(x+y)=45°;
(2)由(1)可得2x+2y+∠CAD+∠CBE=360°,
∵∠CAD+∠CBE=180°-∠ACB=180°-α,
∴2x+2y+180°-α=360°,
∴x+y=90°+
| 1 |
| 2 |
∴∠ECD=180°-(x+y)=180°-(90°+
| 1 |
| 2 |
| 1 |
| 2 |
看了 如图,在△ABC中,∠ACB...的网友还看了以下:
1.已知△ABC,AD平分∠BAC,CE⊥AD交AB于E,EF‖BC,交AC于F.求证∠FEC=∠ 2020-05-16 …
与君同舟渡,达岸各自归.简书漆干未,黯然双泪垂.求这首诗的意思与君同舟渡,达岸各自归.简书漆干未, 2020-05-20 …
急求:如何求各元素的原子个数如:公式Nr(C)=Mr(A)*w(C)/Ar(C)含义是啥上式为求碳 2020-06-04 …
excelA列不含B列两个数的删除ABC12323789123A含有B的两个数C保留237237A 2020-06-14 …
许多淡水鱼在人工饲养条件下不产卵,如果取同种鱼的垂体研碎后注入鱼体内,就可促其产卵,这主要是利用垂 2020-06-20 …
1已知平面abc且a垂直cb垂直ca和b相交l,求证l垂直c~2求证:三个两两垂直的平面的交线也两 2020-06-26 …
AE垂直BC,FG垂直C,角1=角2,角D=角3+60,角CBD=70,求证AB平行CD;求角C的 2020-07-25 …
已知集合AB都含有12个元素,A交B含有4个元素,集合C含有3个元素,且C真包含于A并B,C交B不 2020-07-30 …
在平面直角坐标系中,点A(2,m+1)和点B(m+3,-4)都在直线l上,且直线l∥x轴.(1)求 2020-07-30 …
如图,已知平行四边形ABCD的周长是32cm.BC=3/5AB,AE垂直BC,AF垂直CD,E、F是 2021-02-17 …