早教吧作业答案频道 -->数学-->
如图,△ABC和△CDE是等腰直角三角形,∠BAC=∠CED=∠BCE=90°.点M为BC边上一点,连接EM、BD交于点N,点N恰好是BD中点,连接AN.(1)求证:MN=EN;(2)连接AM、AE,请探究AN与EN的位置关系与
题目详情
如图,△ABC和△CDE是等腰直角三角形,∠BAC=∠CED=∠BCE=90°.点M为BC边上一点,连接EM、BD交于点N,点N恰好是BD中点,连接AN.
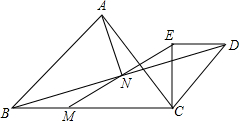
(1)求证:MN=EN;
(2)连接AM、AE,请探究AN与EN的位置关系与数量关系.
①写出AN与EM:位置关系___;数量关系___;
②请证明上述结论.

(1)求证:MN=EN;
(2)连接AM、AE,请探究AN与EN的位置关系与数量关系.
①写出AN与EM:位置关系___;数量关系___;
②请证明上述结论.
▼优质解答
答案和解析
(1)证明:∵∠CED=∠BCE=90°,
∴BC∥DE,
∴∠MBN=∠EDN,
∵点N恰好是BD中点,
∴BN=DN,
在△BMN和△DEN中,
,
∴△BMN≌△DEN(ASA),
∴MN=EN;
(2)①位置关系:AN⊥EM,数量关系:AN=
EM.
故答案为:AN⊥EM,AN=
EM.
②证明:连接AM,AE,
∵△BMN≌△DEN,
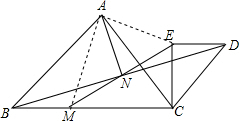 ∴BM=DE,
∴BM=DE,
∵△ABC和△CDE是等腰直角三角形,
∴AB=AC,∠ABM=∠ACB=45°,DE=CE,
∴BM=CE,
∵∠BCE=90°,
∴∠ACE=45°,
∴∠ABM=∠ACE,
在△ABM和△ACE中,
,
∴△ABM≌△ACE(SAS),
∴AM=AE,∠BAM=∠CAE,
∴∠BAM+∠CAM=∠CAE+∠CAM,
即∠MAE=∠BAC=90°,
∵MN=EN,
∴AN⊥EM,AN=
EM.
∴BC∥DE,
∴∠MBN=∠EDN,
∵点N恰好是BD中点,
∴BN=DN,
在△BMN和△DEN中,
|
∴△BMN≌△DEN(ASA),
∴MN=EN;
(2)①位置关系:AN⊥EM,数量关系:AN=
| 1 |
| 2 |
故答案为:AN⊥EM,AN=
| 1 |
| 2 |
②证明:连接AM,AE,
∵△BMN≌△DEN,
 ∴BM=DE,
∴BM=DE,∵△ABC和△CDE是等腰直角三角形,
∴AB=AC,∠ABM=∠ACB=45°,DE=CE,
∴BM=CE,
∵∠BCE=90°,
∴∠ACE=45°,
∴∠ABM=∠ACE,
在△ABM和△ACE中,
|
∴△ABM≌△ACE(SAS),
∴AM=AE,∠BAM=∠CAE,
∴∠BAM+∠CAM=∠CAE+∠CAM,
即∠MAE=∠BAC=90°,
∵MN=EN,
∴AN⊥EM,AN=
| 1 |
| 2 |
看了 如图,△ABC和△CDE是等...的网友还看了以下:
要测量A、B两地的高度差,但不能直接测量,找了D E F G H 5个中间点,测量结果如下表(单位 2020-05-13 …
如图所示,平行金属板A、B之间有匀强电场,A、B间电压为600V,A板带正电并接地,A、B两板间距 2020-05-20 …
如图,D,E是D,A,E三点所在直线m上的两个动点(D,A,E三点互不相重合),且三角形ABF和三 2020-06-13 …
如图,已知圆M:(x-4)2+(y-4)2=4,四边形ABCD为圆M的内接正方形,E、F分别为边A 2020-06-13 …
如图所示的电路中,M、N是两个接线柱,准备连接滑动变阻器,(1)当A接M,D接N时,滑片向右移,电 2020-06-18 …
重组字母为单词e,e,r,w,he,e,r,t,he,e,se,a,sw,m,s,ir,t,p,i 2020-07-09 …
关于电阻决定式中L与S的含义一个边长为a,横截面积为S,电阻率为ρ的正方形导体ABCD,AB、BC 2020-07-29 …
在菱形ABCD中,∠A=60°,以D为顶点作等边三角形DEF,连接EC,点N、P分别为EC、BC的中 2020-11-01 …
如图所示,C为电容器,E为电源,S为单刀双向开关,A为小灯泡,电容器原来不带电,S为断开状态试分析: 2020-11-28 …
如图所示,a、b、c、d为电路中的四个接线点,若用电流表测量通过小灯泡的电流强度,则电流表的M、N接 2020-12-05 …