早教吧作业答案频道 -->数学-->
如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为()A.1B.2C.3D.4
题目详情
如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为( )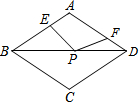
A. 1
B. 2
C. 3
D. 4
▼优质解答
答案和解析
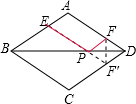 作F点关于BD的对称点F′,则PF=PF′,连接EF′交BD于点P.
作F点关于BD的对称点F′,则PF=PF′,连接EF′交BD于点P.
∴EP+FP=EP+F′P.
由两点之间线段最短可知:当E、P、F′在一条直线上时,EP+FP的值最小,此时EP+FP=EP+F′P=EF′.
∵四边形ABCD为菱形,周长为12,
∴AB=BC=CD=DA=3,AB∥CD,
∵AF=2,AE=1,
∴DF=AE=1,
∴四边形AEF′D是平行四边形,
∴EF′=AD=3.
∴EP+FP的最小值为3.
故选:C.
 作F点关于BD的对称点F′,则PF=PF′,连接EF′交BD于点P.
作F点关于BD的对称点F′,则PF=PF′,连接EF′交BD于点P.∴EP+FP=EP+F′P.
由两点之间线段最短可知:当E、P、F′在一条直线上时,EP+FP的值最小,此时EP+FP=EP+F′P=EF′.
∵四边形ABCD为菱形,周长为12,
∴AB=BC=CD=DA=3,AB∥CD,
∵AF=2,AE=1,
∴DF=AE=1,
∴四边形AEF′D是平行四边形,
∴EF′=AD=3.
∴EP+FP的最小值为3.
故选:C.
看了 如图,在周长为12的菱形AB...的网友还看了以下:
若4乘64的a+1次方乘256的a+2次方=4的61次方,求以x为未知数的方程3x+5=a(x-1 2020-04-27 …
设f(x)=ex-a(x+1).(1)若a>0,f(x)≥0对一切x∈R恒成立,求a的最大值;(2 2020-05-15 …
已知(a-1)的a-1方=1,求整数a的值 2020-05-15 …
数列证明题(在线等,完成后在多给分)下面的a(1),a(2),.a(n)都是数组的项.a(n)*2 2020-06-06 …
关于x的不等式2x-a≤-1的解集如图所示,那么a的值是答案是a=-1,因为:x≤2分之a减一,而 2020-06-06 …
已知函数f(x)=x+a/x+b,(x≠0),其中a、b∈R.(1)若曲线y=f(x)在点P(2, 2020-06-08 …
设f(x)=ex-a(x+1).(1)若a>0,f(x)≥0对一切x∈R恒成立,求a的最大值;(2 2020-06-12 …
∫(∞,0)Ae^(-2x)dx怎么算是e的-2x次方.怎么算啊.Ae^(-2x)的导数又是怎么算 2020-06-14 …
c++求解释下面式子中*((a+1)[1])=*(*((a+1)+1))怎么来的*(a+1)[1] 2020-06-15 …
y=a^1/x的图像是什么样子的?a>1和0>a>1两种 2020-06-19 …