早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠C=90°,以BC为直径的O交斜边AB于点M,若H是AC的中点,连接MH.(1)求证:MH为O的切线.(2)若MH=32,tan∠ABC=34,求O的半径.(3)在(2)的条件下分别过点A、B作O的
题目详情
如图,在Rt△ABC中,∠C=90°,以BC为直径的 O交斜边AB于点M,若H是AC的中点,连接MH.
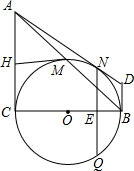
(1)求证:MH为 O的切线.
(2)若MH=
,tan∠ABC=
,求 O的半径.
(3)在(2)的条件下分别过点A、B作 O的切线,两切线交于点D,AD与 O相切于N点,过N点作NQ⊥BC,垂足为E,且交 O于Q点,求线段NQ的长度.

(1)求证:MH为 O的切线.
(2)若MH=
| 3 |
| 2 |
| 3 |
| 4 |
(3)在(2)的条件下分别过点A、B作 O的切线,两切线交于点D,AD与 O相切于N点,过N点作NQ⊥BC,垂足为E,且交 O于Q点,求线段NQ的长度.
▼优质解答
答案和解析
(1)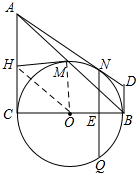 连接OH、OM,
连接OH、OM,
∵H是AC的中点,O是BC的中点,
∴OH是△ABC的中位线,
∴OH∥AB,
∴∠COH=∠ABC,∠MOH=∠OMB,
又∵OB=OM,
∴∠OMB=∠MBO,
∴∠COH=∠MOH,
在△COH与△MOH中,
,
∴△COH≌△MOH(SAS),
∴∠HCO=∠HMO=90°,
∴MH是 O的切线;
(2)∵MH、AC是 O的切线,
∴HC=MH=
,
∴AC=2HC=3,
∵tan∠ABC=
,
∴
=
,
∴BC=4,
∴ O的半径为2;
(3)连接OA、CN、ON,OA与CN相交于点I,
∵AC与AN都是 O的切线,
∴AC=AN,AO平分∠CAD,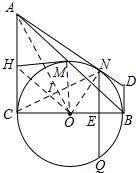
∴AO⊥CN,
∵AC=3,OC=2,
∴由勾股定理可求得:AO=
,
∵
AC•OC=
AO•CI,
∴CI=
,
∴由垂径定理可求得:CN=
,
设OE=x,
由勾股定理可得:CN2-CE2=ON2-OE2,
∴
-(2+x)2=4-x2,
∴x=
,
∴CE=
,
由勾股定理可求得:EN=
,
∴由垂径定理可知:NQ=2EN=
.
 连接OH、OM,
连接OH、OM,∵H是AC的中点,O是BC的中点,
∴OH是△ABC的中位线,
∴OH∥AB,
∴∠COH=∠ABC,∠MOH=∠OMB,
又∵OB=OM,
∴∠OMB=∠MBO,
∴∠COH=∠MOH,
在△COH与△MOH中,
|
∴△COH≌△MOH(SAS),
∴∠HCO=∠HMO=90°,
∴MH是 O的切线;
(2)∵MH、AC是 O的切线,
∴HC=MH=
| 3 |
| 2 |
∴AC=2HC=3,
∵tan∠ABC=
| 3 |
| 4 |
∴
| AC |
| BC |
| 3 |
| 4 |
∴BC=4,
∴ O的半径为2;
(3)连接OA、CN、ON,OA与CN相交于点I,
∵AC与AN都是 O的切线,
∴AC=AN,AO平分∠CAD,

∴AO⊥CN,
∵AC=3,OC=2,
∴由勾股定理可求得:AO=
| 13 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CI=
6
| ||
| 13 |
∴由垂径定理可求得:CN=
12
| ||
| 13 |
设OE=x,
由勾股定理可得:CN2-CE2=ON2-OE2,
∴
| 144 |
| 13 |
∴x=
| 10 |
| 13 |
∴CE=
| 10 |
| 13 |
由勾股定理可求得:EN=
| 24 |
| 13 |
∴由垂径定理可知:NQ=2EN=
| 48 |
| 13 |
看了 如图,在Rt△ABC中,∠C...的网友还看了以下:
肯定属于同族元素且性质相似的是()A.原子核外电子排布式:A为1s22s2,B为1s2B.结构示意 2020-05-13 …
肯定属于同族元素且性质相似的是()A.原子核外电子排布式:A为1s22s2,B为1s2B.结构示意 2020-05-14 …
有一道题说A和B能形成铁的合金,而A为黑色固体单质.我看解析上说:铁的合金中含有铁和碳,又因为A为 2020-05-17 …
两个物块A,B.A在B上放着,A为mg,B为2mg,且它们之间的摩擦因数为u,那么它们之间...两 2020-05-24 …
探讨数轴上两点之间的距离已知数轴上有两个点A、B,求A、B之间的距离:(1)当A为+2,B为+3时 2020-06-27 …
若0小于a小于b小于1,试确定log以a为底b的对数log以b为底a的对数,log以b分之1为底a 2020-06-30 …
A、B、C、D、E五种物质在一定条件下的转化关系如图所示.若A在常温下为气态单质,则A为;B为;C 2020-07-12 …
已知:log以a为底b的对数=log以b为底a的对数(a>0,a≠1;b>0,b≠1),求证:a= 2020-07-29 …
请阅读材料:①一般地,n个相同的因数a相乘:记为an,如23=8,此时,指数3叫做以2为底8的对数 2020-07-30 …
1在锐角三角形ABC中,若a为4,b为3,边长c的取值范围2在三角形ABC中,A,B,C,的对边分别 2020-10-31 …