早教吧作业答案频道 -->数学-->
若关于x的方程(x-2)2ex+ae-x=2a|x-2|(e为自然对数的底数)有且仅有6个不等的实数解,则实数a的取值范围是()A.(e22e-1,+∞)B.(e,+∞)C.(1,e)D.(1,e22e-1)
题目详情
若关于x的方程(x-2)2ex+ae-x=2a|x-2|(e为自然对数的底数)有且仅有6个不等的实数解,则实数a的取值范围是( )
A. (
,+∞)e2 2e-1
B. (e,+∞)
C. (1,e)
D. (1,
)e2 2e-1
▼优质解答
答案和解析
∵(x-2)2ex+ae-x=2a|x-2|,
∴(x-2)2e2x-2a|x-2|ex+a=0,
令g(x)=|x-2|ex=
,则g′(x)=
,
∴当x≥2或x<1时,g′(x)>0,当1<x<2时,g′(x)<0,
∴g(x)在(-∞,1)上单调递增,在(1,2)上单调递减,在(2,+∞)上单调递增,
∴当x=1时,g(x)取得极大值t(1)=e,
又x→-∞时,g(x)→0,g(2)=0,x→+∞时,g(x)→+∞,
作出g(x)的函数图象如图所示:
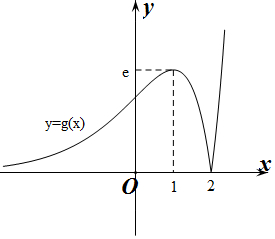
令g(x)=t,
由图象可知:当0<t<e时,方程g(x)=t<有3解;当t=0或t>e时,方程g(x)=t有1解;
当t=e时,方程g(x)=t有2解;当t<0时,方程g(x)=t无解.
∵方程(x-2)2e2x-2a|x-2|ex+a=0有6解,
即g2(x)-2ag(x)+a=0有6解,
∴关于t的方程t2-2at+a=0在(0,e)上有2解,
∴
,解得1<a<
.
故选D.
∴(x-2)2e2x-2a|x-2|ex+a=0,
令g(x)=|x-2|ex=
|
|
∴当x≥2或x<1时,g′(x)>0,当1<x<2时,g′(x)<0,
∴g(x)在(-∞,1)上单调递增,在(1,2)上单调递减,在(2,+∞)上单调递增,
∴当x=1时,g(x)取得极大值t(1)=e,
又x→-∞时,g(x)→0,g(2)=0,x→+∞时,g(x)→+∞,
作出g(x)的函数图象如图所示:

令g(x)=t,
由图象可知:当0<t<e时,方程g(x)=t<有3解;当t=0或t>e时,方程g(x)=t有1解;
当t=e时,方程g(x)=t有2解;当t<0时,方程g(x)=t无解.
∵方程(x-2)2e2x-2a|x-2|ex+a=0有6解,
即g2(x)-2ag(x)+a=0有6解,
∴关于t的方程t2-2at+a=0在(0,e)上有2解,
∴
|
| e2 |
| 2e-1 |
故选D.
看了 若关于x的方程(x-2)2e...的网友还看了以下:
-2A*A--2A的2次方等于多少? 2020-05-13 …
已知点P(1-2a,b+2)关于x轴的对称点和点Q(2,-1)关于y轴的对称点是同一个点,求a、b 2020-05-16 …
(2a的2次方)的三次方乘以(a的二次方)的四次方除以(-2a的二次方)的五次方 2020-06-12 …
已知A=2a的2次方+3ab-2a-1,b=-a的2次方+ab-1,且3A+6B的值与a无关,求b 2020-07-20 …
已知a,b,c是一个三角形的三边,试证明a的4次方+b的4次方+c的4次方-2a的2次方b的2次方 2020-07-20 …
初一下册整式运算学得好的,1.若a²-2a+1=0,则2a²-4a=2.关于x的2次3项式的2次项 2020-07-31 …
(a+b)的2次方(a-b)的2次方-(a的2次方+b的2次方)(a-b)答案是a的4次方-a的3 2020-08-02 …
已知(a-2)x的2次方+(2b+1)xy-x+y-7是关于x,y的多项式,若该多项式不含二次项, 2020-08-03 …
数学题,在线等,急,回答了给QB计算题(写过程)(x+2)(x+3)-(x+6)(x-1)(3a+1 2020-11-03 …
2道数学填空题!1.式子4a的实际意义可解释为().2.式子2a的2次方b的2次方c和3a的2次方b 2020-11-03 …