已知函数f（x）=xlnx-2x，x>0x2+32x，x≤0的图象上有且仅有四个不同的点关于直线y=-1的对称点在y=kx-1的图象上，则实数k的取值范围是（）A.(12，1)B.(12，34)C.(13，1)D.(12，2)

Question

已知函数f（x）=

xlnx-2x，x>0

x2+(3)/(2)x，x≤0

的图象上有且仅有四个不同的点关于直线y=-1的对称点在y=kx-1的图象上，则实数k的取值范围是（　　）

A. (

(1)/(2)，1)

B. (

(1)/(2)，(3)/(4))

C. (

(1)/(3)，1)

D. (

(1)/(2)，2)

Answer 1

∵函数f（x）=

xlnx-2x，x>0

x2+(3)/(2)x，x≤0

的图象上有且仅有四个不同的点关于直线y=-1的对称点在y=kx-1的图象上，
而函数y=kx-1关于直线y=-1的对称图象为y=-kx-1，
∴f（x）=

xlnx-2x，x>0

x2+(3)/(2)x，x≤0

的图象与y=-kx-1的图象有且只有四个不同的交点，
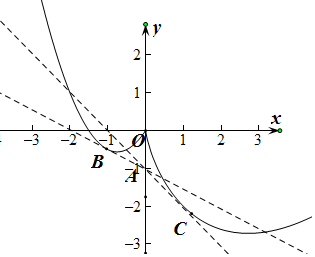
作函数f（x）=

xlnx-2x，x>0

x2+(3)/(2)x，x≤0

的图象与y=-kx-1的图象如下，
易知直线y=-kx-1恒过点A（0，-1），
设直线AC与y=xlnx-2x相切于点C（x，xlnx-2x），
y′=lnx-1，
故lnx-1=(xlnx-2x+1)/(x)，
解得，x=1；
故k_AC=-1；
设直线AB与y=x²+(3)/(2)x相切于点B（x，x²+(3)/(2)x），
y′=2x+(3)/(2)，
故2x+(3)/(2)=(x2+(3)/(2)x+1)/(x)，
解得，x=-1；
故k_AB=-2+(3)/(2)=-(1)/(2)；
故-1<-k<-(1)/(2)，
故(1)/(2)<k<1；
故选：A．