早教吧作业答案频道 -->数学-->
喜欢钻研的小亮对75°角的三角函数发生了兴趣,他想:75度虽然不是特殊角,但和特殊角有着密切的关系,能否通过特殊角的三角函数值求75°的正弦值呢?经研究,他发现:sin75°=sin(45°+30
题目详情
喜欢钻研的小亮对75°角的三角函数发生了兴趣,他想:75度虽然不是特殊角,但和特殊角有着密切的关系,能否通过特殊角的三角函数值求75°的正弦值呢?经研究,他发现:sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°,于是他大胆猜想:sin(α+β)=sinαcosβ+cosαsinβ(α和β为锐角).将图1(a)等积变形为图1(b)可用于勾股定理的证明,现将这两幅图分别“压扁”成图2(a)和图2(b).如图,锐角为α的直角三角形斜边为m,锐角为β的直角三角形斜边为n,请你借助图2(a)和图2(b)证明上述结论能成立.
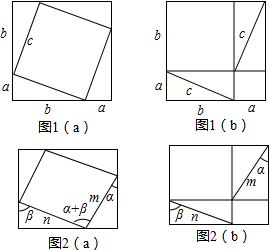 喜欢钻研的小亮对75°角的三角函数发生了兴趣,他想:75度虽然不是特殊角,但和特殊角有着密切的关系,能否通过特殊角的三角函数值求75°的正弦值呢?经研究,他发现:sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°,于是他大胆猜想:sin(α+β)=sinαcosβ+cosαsinβ(α和β为锐角).将图1(a)等积变形为图1(b)可用于勾股定理的证明,现将这两幅图分别“压扁”成图2(a)和图2(b).如图,锐角为α的直角三角形斜边为m,锐角为β的直角三角形斜边为n,请你借助图2(a)和图2(b)证明上述结论能成立.
喜欢钻研的小亮对75°角的三角函数发生了兴趣,他想:75度虽然不是特殊角,但和特殊角有着密切的关系,能否通过特殊角的三角函数值求75°的正弦值呢?经研究,他发现:sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°,于是他大胆猜想:sin(α+β)=sinαcosβ+cosαsinβ(α和β为锐角).将图1(a)等积变形为图1(b)可用于勾股定理的证明,现将这两幅图分别“压扁”成图2(a)和图2(b).如图,锐角为α的直角三角形斜边为m,锐角为β的直角三角形斜边为n,请你借助图2(a)和图2(b)证明上述结论能成立.


 喜欢钻研的小亮对75°角的三角函数发生了兴趣,他想:75度虽然不是特殊角,但和特殊角有着密切的关系,能否通过特殊角的三角函数值求75°的正弦值呢?经研究,他发现:sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°,于是他大胆猜想:sin(α+β)=sinαcosβ+cosαsinβ(α和β为锐角).将图1(a)等积变形为图1(b)可用于勾股定理的证明,现将这两幅图分别“压扁”成图2(a)和图2(b).如图,锐角为α的直角三角形斜边为m,锐角为β的直角三角形斜边为n,请你借助图2(a)和图2(b)证明上述结论能成立.
喜欢钻研的小亮对75°角的三角函数发生了兴趣,他想:75度虽然不是特殊角,但和特殊角有着密切的关系,能否通过特殊角的三角函数值求75°的正弦值呢?经研究,他发现:sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°,于是他大胆猜想:sin(α+β)=sinαcosβ+cosαsinβ(α和β为锐角).将图1(a)等积变形为图1(b)可用于勾股定理的证明,现将这两幅图分别“压扁”成图2(a)和图2(b).如图,锐角为α的直角三角形斜边为m,锐角为β的直角三角形斜边为n,请你借助图2(a)和图2(b)证明上述结论能成立.

▼优质解答
答案和解析
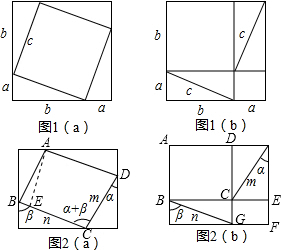 如图2(a),原来内部的正方形变成了一个平行四边形,m,n为相邻两边,其夹角为α+β,
如图2(a),原来内部的正方形变成了一个平行四边形,m,n为相邻两边,其夹角为α+β,
作▱ABCD的高AE,则AE=AB•sinB=msin(180°-α-β)=msin(α+β),
则S▱ABCD▱ABCD=BC•AE=n•msin(α+β)=mnsin(α+β).
如图2(b),原来的两个小正方形变成了两个矩形ABCD与CEFG,
则S矩形ABCD矩形ABCD=BC•AB=nsinβ•mcosα=mncosαsinβ,
S矩形CEFG矩形CEFG=CE•CG=msinα•ncosβ=mnsinαcosβ,
∵图2(a)与图2(b)中空白部分的面积相等,
∴mnsin(α+β)=mncosαsinβ+mnsinαcosβ,
化简得sin(α+β)=sinαcosβ+cosαsinβ.
 如图2(a),原来内部的正方形变成了一个平行四边形,m,n为相邻两边,其夹角为α+β,
如图2(a),原来内部的正方形变成了一个平行四边形,m,n为相邻两边,其夹角为α+β,作▱ABCD的高AE,则AE=AB•sinB=msin(180°-α-β)=msin(α+β),
则S▱ABCD▱ABCD=BC•AE=n•msin(α+β)=mnsin(α+β).
如图2(b),原来的两个小正方形变成了两个矩形ABCD与CEFG,
则S矩形ABCD矩形ABCD=BC•AB=nsinβ•mcosα=mncosαsinβ,
S矩形CEFG矩形CEFG=CE•CG=msinα•ncosβ=mnsinαcosβ,
∵图2(a)与图2(b)中空白部分的面积相等,
∴mnsin(α+β)=mncosαsinβ+mnsinαcosβ,
化简得sin(α+β)=sinαcosβ+cosαsinβ.
看了 喜欢钻研的小亮对75°角的三...的网友还看了以下:
请填写表格(要求书写认真,卷面整洁)种类生殖特点发育特点昆虫有性生殖,受精,卵生发育和发育两栖动物 2020-04-08 …
已知sin阿发=5分之,sinβ=5分之4,且阿发β都是锐角,阿发+β=什么?是已知sin阿发=- 2020-05-14 …
4.discoverv.→n.发现;发觉5.wiseadj.→adv.聪明地;明智地6.stran 2020-05-16 …
四年级1班有若干本练习本要发给同学们.若每人发5本,还剩7本;每人发7本,刚还差5本,有几名同学? 2020-05-17 …
科学发现:植物的花瓣、萼片、果实的数目以及其他方面的特征,都非常吻合于一个奇特的数列--著名的裴波 2020-05-17 …
CMM包括5个成熟等级,开发的能力越强,开发组织的成熟度越高,等级越高。其中,可重复级的特点是___ 2020-05-26 …
2003年5月13日,安徽淮北芦岭煤矿发生特大瓦斯爆炸事故,造成86人死亡、28人受伤.此前,贵州 2020-06-17 …
下列关于特异性免疫和非特异性免疫的叙述中,不正确的是[]A.发生非特异性免疫的结构主要是皮肤、黏膜 2020-06-19 …
2008年5月12日在四川汶川发生特大地震,给当地造成严重灾害,育才小学掀起抗灾捐款活动.六(1) 2020-06-25 …
设某地区历史上从某次特大洪水发生以后,在30年内发生特大洪水的概率是0.8,在40年内发生特大洪水 2020-06-30 …