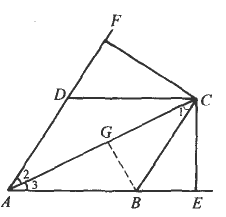
如图，从ABCD的顶点C向AB和AD的延长线引垂线CE和CF，垂足分别为E、F．求证：AB·AE＋AD·AF＝AC2．

Question

如图，从 ABCD的顶点C向AB和AD的延长线引垂线CE和CF，垂足分别为E、F．求证：AB·AE＋AD·AF＝AC ² ．

Answer 1

答案：
解析：
　　证明：作BG⊥AC于G，则 　　∵∠3＝∠3，∠BGA＝∠CEA＝， 　　∴△ABG∽△ACE． 　　∴＝． 　　∴AC·AG＝AB·AE．① 　　又∵BC∥AD，CF⊥AF， 　　∴∠1＝∠2，∠CGB＝∠CFA＝， 　　∴△CBG∽△ACF． 　　∴＝． 　　∴AC·CG＝CB·AF② 　　①＋②，得 　　AC2＝AC(AG＋CG)＝AC·AG＋AC·CG 　　＝AE·AB＋AF·BC．
提示：
　　点悟：等式左边两项均为两线段之积，而右边为AC2，故应设法将AC2拆成两线段积的形式，而AC并不能表示成两条线段的比例中项，但AC2＝AC(AG＋GC)＝AC·AG＋AC·GC，只需AC·AG和AC·GC与左端两项分别相等即可(作BG⊥AC于G)． 　　点拨：一般地，要证形如ab＝cd＋ef的线段关系，常常在a(或b)上取一点P，使ab化为两项和的形式，然后利用比例中的有关定理，在等式两边的对应项之间建立相等关系．