早教吧作业答案频道 -->数学-->
观察发现(1)如图1,若点A、B在直线l同侧,在直线l上找一点P,使AP+BP的值最小.作法如下:作点B关于直线l的对称点B′,连接AB′,与直线l的交点就是所求的点P.(2)如图2,在等边
题目详情
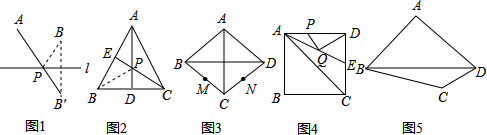
【观察发现】(1)如图1,若点A、B在直线l同侧,在直线l上找一点P,使AP+BP的值最小.作法如下:作点B关于直线l的对称点B′,连接AB′,与直线l的交点就是所求的点P.
(2)如图2,在等边三角形ABC中,AB=4,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小.
作法如下:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为___.
【实践运用】
如图3,菱形ABCD中,对角线AC、BD分别为6和8,M、N分别是边BC、CD的中点,若点P是BD上的动点,则MP+PN的最小值是___.
【拓展延伸】
(1)如图4,正方形ABCD的边长为5,∠DAC的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则DQ+PQ的最小值是___;
(2)如图5,在四边形ABCD的对角线BD上找一点P,使∠APB=∠CPB.保留画图痕迹,并简要写出画法.
(2)如图2,在等边三角形ABC中,AB=4,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小.
作法如下:作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为___.
【实践运用】
如图3,菱形ABCD中,对角线AC、BD分别为6和8,M、N分别是边BC、CD的中点,若点P是BD上的动点,则MP+PN的最小值是___.
【拓展延伸】
(1)如图4,正方形ABCD的边长为5,∠DAC的平分线交DC于点E.若点P,Q分别是AD和AE上的动点,则DQ+PQ的最小值是___;
(2)如图5,在四边形ABCD的对角线BD上找一点P,使∠APB=∠CPB.保留画图痕迹,并简要写出画法.

▼优质解答
答案和解析
【观察发现】(2)如图
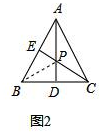
在等边三角形ABC中,AB=4,点E是AB的中点,
∴∠BEC=90°,BE=2,BC=4,
由勾股定理可求:CE=
=2
,
∴BP+PE的最小值为2
;
【实践运用】如图3,
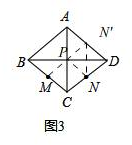
作点N关于BD的对称点N′,连接MN′交BD于点P,此时MP+PN的最小,MP+PN=MN′,
∵菱形ABCD中,M、N分别是边BC、CD的中点,
∴由菱形的轴对称性可知,点N′为AD的中点,
易证MN′=AB,
∵菱形ABCD中,对角线AC、BD分别为6和8,
∴∠APB=90°,AP=3,BP=4,
由勾股定理可求,AB=
=5,
∴MN′=AB=5,
∴MP+PN的最小值是5;
【拓展延伸】(1)如图4,
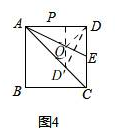
作点D关于AE的对称点D′,
∵AE是∠DAC的平分线,
∴点D′在AD上,
过点D′作D′P⊥AD,交AE于点Q,此时DQ+PQ最小,DQ+PQ=D′P,
∵正方形ABCD的边长为5,
∴AD′=5,∠D′AP=45°,
∴
=sin45°=
,
解得;D′P=
,
∴DQ+PQ的最小值是
;
(2)
如图5,
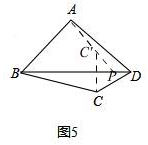
作点C关于BD的对称点C′,连接AC′并延长交于BD于点P,则点P即为所求.
【观察发现】(2)如图
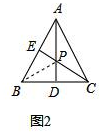
在等边三角形ABC中,AB=4,点E是AB的中点,
∴∠BEC=90°,BE=2,BC=4,
由勾股定理可求:CE=
| BC2-BE2 |
| 3 |
∴BP+PE的最小值为2
| 3 |
【实践运用】如图3,

作点N关于BD的对称点N′,连接MN′交BD于点P,此时MP+PN的最小,MP+PN=MN′,
∵菱形ABCD中,M、N分别是边BC、CD的中点,
∴由菱形的轴对称性可知,点N′为AD的中点,
易证MN′=AB,
∵菱形ABCD中,对角线AC、BD分别为6和8,
∴∠APB=90°,AP=3,BP=4,
由勾股定理可求,AB=
| 32+42 |
∴MN′=AB=5,
∴MP+PN的最小值是5;
【拓展延伸】(1)如图4,

作点D关于AE的对称点D′,
∵AE是∠DAC的平分线,
∴点D′在AD上,
过点D′作D′P⊥AD,交AE于点Q,此时DQ+PQ最小,DQ+PQ=D′P,
∵正方形ABCD的边长为5,
∴AD′=5,∠D′AP=45°,
∴
| D′P |
| AD′ |
| ||
| 2 |
解得;D′P=
5
| ||
| 2 |
∴DQ+PQ的最小值是
5
| ||
| 2 |
(2)
如图5,

作点C关于BD的对称点C′,连接AC′并延长交于BD于点P,则点P即为所求.
看了 观察发现(1)如图1,若点A...的网友还看了以下:
关于重力,..问题有点刁钻...重力的方向为什么是竖直向下?是实验得到的?总是听老师不停地给我们辨 2020-06-09 …
如图,一辆小车沿固定斜面匀速下滑,在小车下滑的过程中,小车支架上固定着小球的轻杆保持水平.有关小球 2020-06-20 …
大小调关系很晕我对大调小调的关系特别模糊,什么自然大小调啊,关系大小调啊都分不明白他们直接到底怎么 2020-06-20 …
关于混凝土施工规范里的一句话输送泵管倾斜或垂直向下输送混凝土,且高差大于20m时,应在倾斜或垂直管 2020-06-22 …
由三个质量相等的小球a、b、c,以相同的速度从同一高度,分别沿竖直向上、水平和竖直向下抛出.则从抛 2020-07-05 …
以下关于排序的说法中,正确的是()A.排序就是将数按从小到大的顺序排序B.排序只有两种方法,即直以 2020-07-23 …
设小圆直经为r,如果由x个组成一个大圆.求大圆直经与小圆直经的关系?是x个小圆组成一个大圆要是实心 2020-07-29 …
关于角说法正确的下列说法①一条直线就是一个平角②周角就是一条射线③角的两边可以一样长也可以一长一短 2020-07-30 …
关于压力,下列说法中正确的是()A.压力的方向总是竖直向下的B.压力有时就是物体受到的重力C.压力的 2020-12-15 …
下列有关运动的说法正确的是:()A.图甲中撤掉挡板A的瞬间,小球的加速度竖直向下B.图乙中固定在竖直 2021-01-22 …