早教吧作业答案频道 -->数学-->
如图,在平行四边形ABCD中,∠BAD=45°.分别以BC、CD为边向外作△BCF和△DCE,使BF=BC,DE=DC,∠FBC=∠CDE,延长AB交边FC于点H,点H在F、C两点之间,连结AE、AF、DF.(1)求证:△ABF≌△EDA.(2
题目详情
如图,在平行四边形ABCD中,∠BAD=45°.分别以BC、CD为边向外作△BCF和△DCE,使BF=BC,DE=DC,∠FBC=∠CDE,延长AB交边FC于点H,点H在F、C两点之间,连结AE、AF、DF.
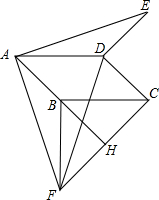
(1)求证:△ABF≌△EDA.
(2)当AE⊥AF时,求∠FBH的度数.
(3)在(2)的条件下,若B为AH的中点,求sin∠ADF的值.

(1)求证:△ABF≌△EDA.
(2)当AE⊥AF时,求∠FBH的度数.
(3)在(2)的条件下,若B为AH的中点,求sin∠ADF的值.
▼优质解答
答案和解析
(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠ABC=∠ADC,
∵BF=BC,DE=DC,∠FBC=∠CDE,
∴AB=ED,FB=AD,∠ABF=∠EDA,
在△ABF和△EDA中,
,
∴△ABF≌△EDA(SAS);
(2)∵△ABF≌△EDA,
∴∠AFB=∠DAE,
∵AE⊥AF,∠BAD=45°,
∴∠FAB+∠DAE=90°-∠BAD=45°,
∴∠FBH=∠FAB+∠AFB=∠FAB+∠DAE=45°;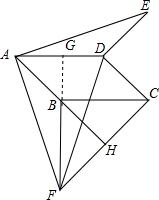
(3)∵△ABF≌△EDA,
∴AD=BF,DE=AB,
∵BF=BC,DE=DC,
∴AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CBH=∠BAD=45°,
∴∠FBC=90°,
延长FB交AD于G,
∴∠DGB=∠FBC=90°,
∴△ABG与△BHF是等腰直角三角形,
设AG=BG=x,
∴AB=BH=
x,
∴BF=AD=2x,
∴DG=x,GF=3x,
∴DF=
x,
∴sin∠ADF=
=
=
.
∴AD=BC,AB=CD,∠ABC=∠ADC,
∵BF=BC,DE=DC,∠FBC=∠CDE,
∴AB=ED,FB=AD,∠ABF=∠EDA,
在△ABF和△EDA中,
|
∴△ABF≌△EDA(SAS);
(2)∵△ABF≌△EDA,
∴∠AFB=∠DAE,
∵AE⊥AF,∠BAD=45°,
∴∠FAB+∠DAE=90°-∠BAD=45°,
∴∠FBH=∠FAB+∠AFB=∠FAB+∠DAE=45°;

(3)∵△ABF≌△EDA,
∴AD=BF,DE=AB,
∵BF=BC,DE=DC,
∴AD=BC,AB=CD,
∴四边形ABCD是平行四边形,
∴AD∥BC,
∴∠CBH=∠BAD=45°,
∴∠FBC=90°,
延长FB交AD于G,
∴∠DGB=∠FBC=90°,
∴△ABG与△BHF是等腰直角三角形,
设AG=BG=x,
∴AB=BH=
| 2 |
∴BF=AD=2x,
∴DG=x,GF=3x,
∴DF=
| 10 |
∴sin∠ADF=
| GF |
| DF |
| 3x | ||
|
3
| ||
| 10 |
看了 如图,在平行四边形ABCD中...的网友还看了以下:
在梯形ABCD中,AD//BC,若AB=DC,E、F分别是CD和BC边上的点,以EF为对称轴翻折梯 2020-05-16 …
在等腰梯形ABCD中,AD‖BC,E为AB的中点,过点E作EF‖BC交CD于点F.AB=4,BC= 2020-05-16 …
一道数学题,急2急,望速解在梯形ABCD中,AD∥BC,AB=DC,E,F分别是边AB和BC上的点 2020-05-16 …
根据下列条件,能画出唯一的三角形ABC的是A.AB=3,BC=4,AC=4B.AB=4,BC=根据 2020-05-24 …
一道是:在等腰梯形ABCD中,AD∥BC,对角线AC⊥BD与点O,AE⊥BC,DF⊥BC,垂足分别 2020-06-05 …
如图,在矩形ABCD中,AB=4,BC=25/2,O为BC上一点,BO=7/2如图所示,以BC所在 2020-06-12 …
用八下的知识解不要用相似1.有一张矩形纸片ABCD,AB=9cm,BC=12cm,将纸片沿EF折叠 2020-06-17 …
在梯形ABCD,AD平行BC,EF分别为AB.CD上的一点,且梯形AEFD……过程最加100,1. 2020-08-01 …
如图1,在等腰梯形ABCD中,AD平行BC,E是AB的中点,过点E作EF平行BC交CD于点F.AB 2020-08-02 …
RT三角形ABC中,∠C=90°,AC=4,BC=5,D为BC边上一点,CD=3,点P在边AC上(P 2020-12-07 …