早教吧作业答案频道 -->数学-->
如图,在矩形ABCD中,E为CD上一点,将△ADE沿直线AE翻折,使点D落在BC边上点D′处(1)如图1,求证:△CD′E~△BAD′;(2)如图2,F为AD上一点,且DF=CD′,EF与BD相交于点G,试探究EF与BD的位
题目详情
如图,在矩形ABCD中,E为CD上一点,将△ADE沿直线AE翻折,使点D落在BC边上点D′处
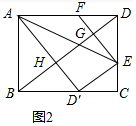
(1)如图1,求证:△CD′E~△BAD′;
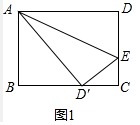
(2)如图2,F为AD上一点,且DF=CD′,EF与BD相交于点G,试探究EF与BD的位置关系,并说明理由;
(3)设AD′与BD相交于点H,在(2)的条件下,若D′E∥BD,HG=2,求BD的长.
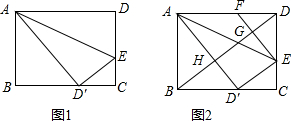
(1)如图1,求证:△CD′E~△BAD′;
(2)如图2,F为AD上一点,且DF=CD′,EF与BD相交于点G,试探究EF与BD的位置关系,并说明理由;
(3)设AD′与BD相交于点H,在(2)的条件下,若D′E∥BD,HG=2,求BD的长.

▼优质解答
答案和解析
(1)证明:如图1中,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵∠AD′E=∠D=90°,
∴∠AD′B+∠ED′C=90°,∠ED′C+∠D′EC=90°,
∴∠AD′B=∠D′EC,
∴△CD′E~△BAD′.
(2) 结论:EF⊥BD,理由如下:
如图2中,
∵△CD′E~△BAD′,
∴
=
,
∵CD′=DF,AD′=AD,D′E=DE
∴
=
,∵∠EDF=∠BAD=90°,
∴△EDF∽△DAB,
∴∠FED=∠ADB,
∵∠ADB+∠BDC=90°,
∴∠FED+∠BDC=90°,
∴∠DGE=90°,
∴EF⊥BD.
(3) ∵D′E∥BD,AD′⊥D′E,
∴BD⊥AD′,
∴∠GHD′=∠HD′E=∠HGE=90°,
∴四边形HGED′是矩形,
∴HG=ED′=DE=2,设EC=y,CD′=x,
易知△DGE≌△ECD′,
∴DG=CE=y,EG=CD′=HD′=x,
∵△BHD′∽△D′CE,
∴
=
,
∴
=
,
∴BH=
,
∴BD=BH+GH+DG=y+2+
,
∵△DFE∽△CED′,
∴
=
,
∴
=
,
∴x2=2y,
∵x2+y2=4,
∴y2+2y-4=0,
∴y=-1+
或-1-
(舍弃),
∴BD=-1+
+2+2=3+
.

∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵∠AD′E=∠D=90°,
∴∠AD′B+∠ED′C=90°,∠ED′C+∠D′EC=90°,
∴∠AD′B=∠D′EC,
∴△CD′E~△BAD′.
(2) 结论:EF⊥BD,理由如下:
如图2中,

∵△CD′E~△BAD′,
∴
| D′E |
| AD′ |
| CD′ |
| BA |
∵CD′=DF,AD′=AD,D′E=DE
∴
| DE |
| AD |
| DF |
| BA |
∴△EDF∽△DAB,
∴∠FED=∠ADB,
∵∠ADB+∠BDC=90°,
∴∠FED+∠BDC=90°,
∴∠DGE=90°,
∴EF⊥BD.
(3) ∵D′E∥BD,AD′⊥D′E,
∴BD⊥AD′,
∴∠GHD′=∠HD′E=∠HGE=90°,
∴四边形HGED′是矩形,
∴HG=ED′=DE=2,设EC=y,CD′=x,
易知△DGE≌△ECD′,
∴DG=CE=y,EG=CD′=HD′=x,
∵△BHD′∽△D′CE,
∴
| BH |
| CD′ |
| HD′ |
| EC |
∴
| BH |
| x |
| x |
| y |
∴BH=
| x2 |
| y |
∴BD=BH+GH+DG=y+2+
| x2 |
| y |
∵△DFE∽△CED′,
∴
| DF |
| EC |
| DE |
| CD′ |
∴
| x |
| y |
| 2 |
| x |
∴x2=2y,
∵x2+y2=4,
∴y2+2y-4=0,
∴y=-1+
| 5 |
| 5 |
∴BD=-1+
| 5 |
| 5 |
看了 如图,在矩形ABCD中,E为...的网友还看了以下:
求一道反比例函数题已知函数y=y1-y2(1与2为下标这里打不出来.下同),其中y1与x成正比例, 2020-05-13 …
设f(x)是定义在区间负无穷到正无穷上以2为周期的函数,对K属于整数,用I*k表示区间2k-1,2 2020-05-20 …
已知f(x)是定义在R上以2为周期的函数,对k∈Z,用I(k)表示区间(2k-1,2k+1].已知 2020-05-20 …
设f(x)是定义在R上以2为周期的奇函数,已知当x∈(0,1)时,f(x)=lg11−x,f(x) 2020-06-06 …
如图所示,半径为R,质量为M的圆柱体放置在水平地面上,与高为h的台阶接触,接触部位够粗糙,现在圆柱 2020-07-01 …
1.为什么气体受热后密度减小,热气为什么会上升?2..为什么气体遇冷后密度增大,冷气为什么会下降? 2020-07-04 …
读下面三个国家轮廓图,回答:(1)俄罗斯和加拿大的北部有很大一部分位于圈以北的带.加拿大的西北部陆 2020-07-05 …
设f(x)是定义在(-∞,+∞)上以2为周期的周期函数,且f(x)是偶函数,在区间[2,3]上,f 2020-07-08 …
在数轴上与-2所对应的点相距4个单位长度的点表示的数是. 2020-07-20 …
设f(x)是定义在区间上以2为周期的函数,对,用表示区间已知当时,f(x)=x2.(1)求f(x) 2020-08-03 …