）如图，已知抛物线经过点A（4，0），B（0，4），C（6，6）．（1）求抛物线的表达式；（2）证明：四边形AOBC的两条对角线互相垂直；（3）在

Question

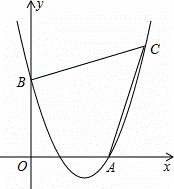
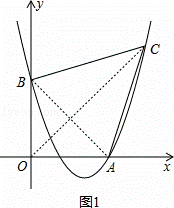
）如图，已知抛物线经过点 A （ 4 ， 0 ）， B （ 0 ， 4 ）， C （ 6 ， 6 ）．

（ 1 ）求抛物线的表达式；

（ 2 ）证明：四边形 AOBC 的两条对角线互相垂直；

（ 3 ）在四边形 AOBC 的内部能否截出面积最大的 ▱ DEFG ？（顶点 D ， E ， F ， G 分别在线段 AO ， OB ， BC ， CA 上，且不与四边 形 AOBC 的顶点重合）若能，求出 ▱ DEFG 的最大面积，并求出此时点 D 的坐标；若不能，请说明理由．

Answer 1

  （ 1 ）设该抛物线的解析式为 y=ax ² +bx+c ，

根据题意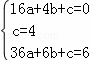得 ，解得 ，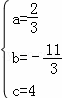

∴ 抛物线的表达式为 y= x ² ﹣ x +4 ；

（ 2 ）如图 1 ，连结 AB 、 OC ，

∵ A （ 4 ， 0 ）， B （ 0 ， 4 ）， C （ 6 ， 6 ），

∴ OA=4 ， OB=4 ， CB= =2 ， CA= =2 ，

∴ OA=OB ， CA=CB ，

∴ OC 垂直平分 AB ，

即四边形 AOBC 的两条对角线互相垂直；

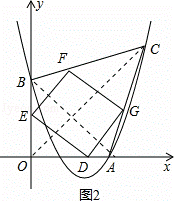
（ 3 ）能．

如图 2 ， AB= =4 ， OC= =6 ，设 D （ t ， 0 ），

∵ 四边形 DEFG 为平行四边形，

∴ EF ∥ DG ， EF=DG ，

∵ OC 垂直平分 AB ，

∴△ OBC 与 △ OAC 关于 OC 对称，

∴ EF 和 DG 为对应线段，

∴ 四边形 DEFG 为矩形， DG ∥ OC ，

∴ DE ∥ AB ，

∴△ ODE ∽△ OAB ，

∴ = ，即 = ，解得 DE= t ，

∵ DG ∥ OC ，

∴△ ADG ∽△ AOC ，

∴ = ，即 = ，解得 DG= （ 4 ﹣ t ），

∴ 矩形 DEFG 的面积 =DE•DG= t• （ 4 ﹣ t ） = ﹣ 3t ² +12t= ﹣ 3 （ t ﹣ 2 ） ² +12 ，

当 t=2 时，平行四边形 DEFG 的面积最大，最大值为 12 ，此时 D 点坐标为（ 2 ， 0 ）．