早教吧作业答案频道 -->数学-->
函数f(x)=(0≤x≤2π)的最小值为()A.B.C.0D.
题目详情
函数f(x)=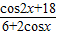 (0≤x≤2π)的最小值为( )
(0≤x≤2π)的最小值为( )
A.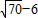
B.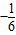
C.0
D.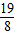
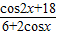 (0≤x≤2π)的最小值为( )
(0≤x≤2π)的最小值为( )A.
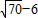
B.
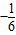
C.0
D.
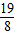
▼优质解答
答案和解析
分析:
先由f(x)=,得f(x)=,再设6+2cosx=t,其中4≤t≤8.则有y=+-6.根据函数单调性与导数的关系,需要求出导函数并令其等于零得到x的值,然后讨论函数的增减性来判断函数的极值,得到函数的最小值即可.
由f(x)=,得f(x)=,设6+2cosx=t,则4≤t≤8.∴y==+-6.得y′=-,令y'=0,得t=,当4≤t<时,f'(x)<0,f(x)在[4,)单调递减∴f(x)在[4,8]单调递减故函数y=+-6在t=8时取得极小值,也是最小值f(x)min=(+-6)=.故选D.
点评:
本题考查了函数的导数运算,研究函数的最值问题.考查应用所学导数的知识、思想和方法解决实际问题的能力,建立函数式、解方程、不等式、最大值等基础知识.
分析:
先由f(x)=,得f(x)=,再设6+2cosx=t,其中4≤t≤8.则有y=+-6.根据函数单调性与导数的关系,需要求出导函数并令其等于零得到x的值,然后讨论函数的增减性来判断函数的极值,得到函数的最小值即可.
由f(x)=,得f(x)=,设6+2cosx=t,则4≤t≤8.∴y==+-6.得y′=-,令y'=0,得t=,当4≤t<时,f'(x)<0,f(x)在[4,)单调递减∴f(x)在[4,8]单调递减故函数y=+-6在t=8时取得极小值,也是最小值f(x)min=(+-6)=.故选D.
点评:
本题考查了函数的导数运算,研究函数的最值问题.考查应用所学导数的知识、思想和方法解决实际问题的能力,建立函数式、解方程、不等式、最大值等基础知识.
看了 函数f(x)=(0≤x≤2π...的网友还看了以下:
函数f(x)在定义域R上不是常数函数,且f(x)满足对任意x∈R,有f(4+x)=f(4-x),f 2020-05-13 …
如图所示,某同学利用浮力知识测量物体A的密度.他把物体A挂在弹簧测力计下静止时,弹簧测力计的示数为 2020-06-16 …
如图所示,小宁用轻质吸盘等器材估测大气压的大小,她设计的实验方案如下:A.记录弹簧测力计的示数为F 2020-07-01 …
如图所示,小宁用轻质吸盘等器材估测大气压的大小,她设计的实验方案如下:A.记录弹簧测力计的示数为F 2020-07-01 …
如图所示,小刚想估测大气压的大小,实验过程如下:A.记录弹簧测力计的示数为F.B.将蘸水的塑料挂衣 2020-07-01 …
(2014•嘉兴模拟)若函数f(x)(x∈R)是奇函数,函数g(x)(x∈R)是偶函数,则一定成立 2020-07-21 …
已知函数y=f(x)是定义在[a,b]上的减函数,那么y=f-1(x)是()A.在[f(a),f( 2020-08-01 …
设f(x)是连续函数,F(x)是f(x)的原函数,则()A.当f(x)是奇函数时,F(x)必为偶函 2020-08-02 …
10.设奇函数f(x)在[-1,1]上是增函数,且f(-1)=一1.若函数,f(x)≤t2一2at+ 2020-11-07 …
如图所示.将重为G的铝块挂在弹簧测力计上,当它浸没在水中时,弹簧测力计的示数为F.则铝块所受的浮力大 2020-11-08 …