早教吧作业答案频道 -->数学-->
(1)如图①,D是等边三角形ABC的AB边上一个动点(点D与点A,B不重合),连接DC,以DC为边在BC上方作等边三角形DCE,连接AE,求证:∠B=∠EAC;(2)如图②,当动点D运动至等边三角形ABC边BA
题目详情
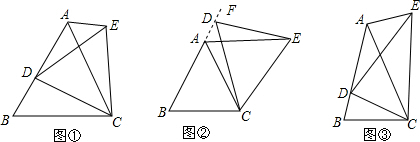
(1)如图①,D是等边三角形ABC的AB边上一个动点(点D与点A,B不重合),连接DC,以DC为边在BC上方作等边三角形DCE,连接AE,求证:∠B=∠EAC;
(2)如图②,当动点D运动至等边三角形ABC边BA的延长线上时,其他作法与(1)相同,(1)中结论∠B=∠EAC还成立吗?请说明理由;
(3)如图③,在等腰三角形ABC中,AB=AC,D是AB上任意一点(点D与A,B不重合),连结CD,以CD为底边作等腰三角形ECD,使顶角∠DEC=∠BAC,连结AE,试探究∠B与∠EAC的数量关系,并说明理由.
(2)如图②,当动点D运动至等边三角形ABC边BA的延长线上时,其他作法与(1)相同,(1)中结论∠B=∠EAC还成立吗?请说明理由;
(3)如图③,在等腰三角形ABC中,AB=AC,D是AB上任意一点(点D与A,B不重合),连结CD,以CD为底边作等腰三角形ECD,使顶角∠DEC=∠BAC,连结AE,试探究∠B与∠EAC的数量关系,并说明理由.

▼优质解答
答案和解析
(1)证明:∵△ABC、△CDE是等边三角形,
∴AB=AC,CD=CE,∠ACB=∠DCE=60°,
∴∠BCD=∠ACE,
∵在△BCD和△ACE中,
∴△BCD≌△ACE(SAS),
∴∠B=∠EAC;
(2) 结论∠B=∠EAC仍成立;
理由如下:∵△ABC、△CDE是等边三角形,
∴AB=AC,CD=CE,∠BCA=∠DCE=60°,
∴∠BCD=∠ACE,
∵在△BCD和△ACE中,
∴△BCD≌△ACE(SAS),
∴∠B=∠EAC;
(3) ∠B=∠EAC;
理由如下:∵AB=AC,ED=EC,顶角∠BAC=∠DEC,
∴底角∠ACB=∠ECD,
∴△ABC∽△EDC,
∴
=
,
又∵∠BCD=∠ACB-∠ACD,∠ACE=∠DCE-∠ACD,
∴∠BCD=∠ACE,
∴△BCD∽△ACE,
∴∠B=∠CAE.
∴AB=AC,CD=CE,∠ACB=∠DCE=60°,
∴∠BCD=∠ACE,
∵在△BCD和△ACE中,
|
∴△BCD≌△ACE(SAS),
∴∠B=∠EAC;
(2) 结论∠B=∠EAC仍成立;
理由如下:∵△ABC、△CDE是等边三角形,
∴AB=AC,CD=CE,∠BCA=∠DCE=60°,
∴∠BCD=∠ACE,
∵在△BCD和△ACE中,
|
∴△BCD≌△ACE(SAS),
∴∠B=∠EAC;
(3) ∠B=∠EAC;
理由如下:∵AB=AC,ED=EC,顶角∠BAC=∠DEC,
∴底角∠ACB=∠ECD,
∴△ABC∽△EDC,
∴
| AC |
| CE |
| BC |
| CD |
又∵∠BCD=∠ACB-∠ACD,∠ACE=∠DCE-∠ACD,
∴∠BCD=∠ACE,
∴△BCD∽△ACE,
∴∠B=∠CAE.
看了 (1)如图①,D是等边三角形...的网友还看了以下:
一辆一辆质量为M的装满沙子的小车以初速度v0在光滑水平面上运动,边运动边漏砂子,当漏掉质量为m的沙 2020-06-12 …
我有道数学题,我不懂啊一动点P在底边长为8CM,腰长为5CM的等腰△ABC的底边BC边上从B向C以 2020-06-27 …
等边三角形OBC的边长为10,点p沿O→B→C→O的方向运动等边三角形OBC的边长为10,点P沿O 2020-07-22 …
如图,点P是等边△ABC的边上的一个作匀速运动的动点,其由点A开始沿AB边运动到B再沿BC边运动到 2020-07-29 …
如图:等边三角形ABC的边长为4cm,点D从点C出发沿CA向A运动,点E从B出发沿AB的延长线BF 2020-08-01 …
如图:等边三角形ABC的边长为4cm,点D从点C出发沿CA向A运动,点E从B出发沿AB的延长线BF 2020-08-01 …
如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB 2020-08-03 …
(2006•汾阳市)如图,点E在正方形ABCD的边CD上运动,AC与BE交于点F.(1)如图1,当点 2020-11-03 …
动点.在等边三角形ABC的边长为4cm,常为1cm的线段MN已知:在等边三角形ABC的边长为4cm, 2020-12-15 …
主动转运与被动转运的根本区别是:A、顺浓度梯度转运B、需借助“载体”或“通道”C、需消耗能量D、转运 2020-12-19 …