早教吧作业答案频道 -->数学-->
如图,在四面体P-ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC=233.(1)求证:PA⊥BD;(2)已知E是PA上一点,且BE∥平面PCD.若PC=2,求点E到平面ABCD的距离.
题目详情
如图,在四面体P-ABCD中,△ABD是边长为2的正三角形,PC⊥底面ABCD,AB⊥BP,BC=
.
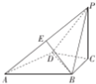
(1)求证:PA⊥BD;
(2)已知E是PA上一点,且BE∥平面PCD.若PC=2,求点E到平面ABCD的距离.
2
| ||
| 3 |

(1)求证:PA⊥BD;
(2)已知E是PA上一点,且BE∥平面PCD.若PC=2,求点E到平面ABCD的距离.
▼优质解答
答案和解析
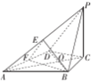 (1)证明:连接AC交BD于O,
(1)证明:连接AC交BD于O,
∵PC⊥BP,BP∩CP=P,
∴PC⊥AB,
∵AB⊥BP,BP∩CP=P,
∴AB⊥平面PBC,
∴AB⊥BC,
∵BC=
,
∴tan∠BAC=
,即∠BAC=30°,
∵∠ABD=60°,
∴∠AOB=90°,
∴AC⊥BD,
∵PC⊥BD,
∴BD⊥平面ACP,
∵AP⊂平面APC,
∴PA⊥BD,
(2)取AD的中点F,连接BF,EF,
当E为PA的中点时,BE∥平面PCD,证明如下,
∵AB=BD,
∴BF⊥AD,
有(1)的BC=CD,则CD⊥AD,
∴EF∥CD,
∵E为PA的中点,
∴EF∥PD,
∴平面BEF∥平面PCD,
∵BE⊂平面BEF,
∴BE∥平面PCD,
∵PC⊥底面ABCD,
∴点E到平面ABCD的距离等于
PC=1
 (1)证明:连接AC交BD于O,
(1)证明:连接AC交BD于O,∵PC⊥BP,BP∩CP=P,
∴PC⊥AB,
∵AB⊥BP,BP∩CP=P,
∴AB⊥平面PBC,
∴AB⊥BC,
∵BC=
2
| ||
| 3 |
∴tan∠BAC=
| ||
| 3 |
∵∠ABD=60°,
∴∠AOB=90°,
∴AC⊥BD,
∵PC⊥BD,
∴BD⊥平面ACP,
∵AP⊂平面APC,
∴PA⊥BD,
(2)取AD的中点F,连接BF,EF,
当E为PA的中点时,BE∥平面PCD,证明如下,
∵AB=BD,
∴BF⊥AD,
有(1)的BC=CD,则CD⊥AD,
∴EF∥CD,
∵E为PA的中点,
∴EF∥PD,
∴平面BEF∥平面PCD,
∵BE⊂平面BEF,
∴BE∥平面PCD,
∵PC⊥底面ABCD,
∴点E到平面ABCD的距离等于
| 1 |
| 2 |
看了 如图,在四面体P-ABCD中...的网友还看了以下:
满足{a}⊆M⊆{a,b,c,d}的集合M的个数是( ) 是{a} {a,b} {a,c} {a, 2020-04-05 …
若非空集合M⊆N={a,b,c,d},则M的个数为8个{a},{b},{c},{d},{a,b}, 2020-05-15 …
#includemain(){inta=0x7fffffff,b=025;floatf1=123. 2020-05-19 …
(1)A,B,C大于0求A/B+3C+B/8C+4A+9C/3A+2B的最小值(2)A,B,C,D 2020-07-09 …
设A=B=D=true,C=false,以下逻辑运算表达式值为真的有()。A.(A∧B)∨(C∧D 2020-07-18 …
1)设a=19^96,b=96^19,c=199^6,d=6^199,则此四数按从小到大的顺序排列 2020-07-18 …
线性代数,如向量a,b,c线性无关,a,b,d线性相关,则()A)a必可由b,c,d线性表示B)b不 2020-11-03 …
a,b,c,d表示4个有理数,已知其中每三个数之和如下:a+b+c=1,a+b+d=-3,a+c+d 2020-11-03 …
求解多元一次不等式的编程47a-b-c-d-e-f-g>047b-a-c-d-e-f-g>023c- 2020-12-14 …
分解因式(b+c-a-d)^4(b-c)(a-d)+(c+a-b-d)^4(c-a)(b-d)+(a 2021-01-04 …