已知以点A（-1，2）为圆心的圆与直线m：x+2y+7=0相切，过点B（-2，0）的动直线与圆A交于M，N两点．（1）求圆A的方程；（2）当|MN|=219时，求直线l的方程．

Question

已知以点A（-1，2）为圆心的圆与直线m：x+2y+7=0相切，过点B（-2，0）的动直线与圆A交于M，N两点．
（1）求圆A的方程；
（2）当|MN|=2√(19)时，求直线l的方程．

Answer 1

（1）由题意知，A（-1，2）到直线x+2y+7=0的距离为圆A半径R，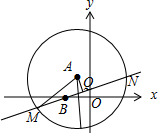
∴R=(|-1+4+7|)/(√(5))=2√(5)，
∴圆A的方程为（x+1）²+（y-2）²=20；
（2）设线段MN的中点为Q，连结QA，则由垂径定理可知∠MQA=90°，且MQ=√(19)，
在Rt△AMQ中，由勾股定理知AQ=√(AM2-MQ2)=1，
当动直线l的斜率不存在时，直线l的方程为x=-2时，显然满足题意；
当动直线l的斜率存在时，设动直线l的方程为：y=k（x+2），
由A（-1，2）到动直线l的距离为1，
得(|-k+2k-2|)/(√(1+k2))=1⇒k=(3)/(4)，
∴y=(3)/(4)(x+2)，即3x-4y+6=0．
∴直线l的方程为3x-4y+6=0或x=-2．