早教吧作业答案频道 -->数学-->
如图,O的半径为1,A,P,B,C是O上的四个点.∠APC=∠CPB=60°.(1)判断△ABC的形状:;(2)当点P位于什么位置时,四边形APBC的面积最大?求出最大面积;(3)直接写出线段PA,PB,
题目详情
如图, O的半径为1,A,P,B,C是 O上的四个点.∠APC=∠CPB=60°.
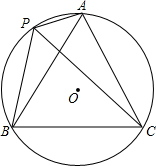
(1)判断△ABC的形状:___;
(2)当点P位于什么位置时,四边形APBC的面积最大?求出最大面积;
(3)直接写出线段PA,PB,PC之间的数量关系.

(1)判断△ABC的形状:___;
(2)当点P位于什么位置时,四边形APBC的面积最大?求出最大面积;
(3)直接写出线段PA,PB,PC之间的数量关系.
▼优质解答
答案和解析
证明:(1)△ABC是等边三角形.
证明如下:在 O中
∵∠BAC与∠CPB是
所对的圆周角,∠ABC与∠APC是
所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
故答案为:等边三角形;
(2)当点P为
的中点时,四边形APBC的面积最大.
理由如下,如图2,过点P作PE⊥AB,垂足为E.
过点C作CF⊥AB,垂足为F.
∵S△APB=
AB•PE,S△ABC=
AB•CF,
∴S四边形APBC=
AB•(PE+CF),
当点P为
的中点时,PE+CF=PC,PC为 O的直径,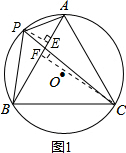
∴此时四边形APBC的面积最大.
又∵ O的半径为1,
∴其内接正三角形的边长AB=
,
∴S四边形APBC=
×2×
=
;
(3)在PC上截取PD=AP,如图2,
又∵∠APC=60°,
∴△APD是等边三角形,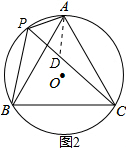
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP.
证明如下:在 O中
∵∠BAC与∠CPB是
 |
| BC |
 |
| AC |
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
故答案为:等边三角形;
(2)当点P为
 |
| AB |
理由如下,如图2,过点P作PE⊥AB,垂足为E.
过点C作CF⊥AB,垂足为F.
∵S△APB=
| 1 |
| 2 |
| 1 |
| 2 |
∴S四边形APBC=
| 1 |
| 2 |
当点P为
 |
| AB |

∴此时四边形APBC的面积最大.
又∵ O的半径为1,
∴其内接正三角形的边长AB=
| 3 |
∴S四边形APBC=
| 1 |
| 2 |
| 3 |
| 3 |
(3)在PC上截取PD=AP,如图2,
又∵∠APC=60°,
∴△APD是等边三角形,

∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
|
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP.
看了 如图,O的半径为1,A,P,...的网友还看了以下:
利用网格作图,(1)请你在图①中画出线段AB关于线段CD所在直线成轴对称的图形;(2)请你在图②中 2020-05-16 …
用电压表测出一段导体两端的电压是72V,用电流表测出通过这段导体的电流为0.4A,则这段导体的电阻 2020-05-21 …
在同一平面内,有八个点,每两点之间连一条线段,最多可连()条线段.思考提示:2个点最多可以连()条 2020-06-14 …
判断:(1)在两点间所有的连线中,线段最短.()(2)同—平面内的两条直线,不平行就—定判断:(1 2020-06-15 …
标出下段中的错别字,然后将正确的汉字依次写在下面的方格内。人类所曾做到的最高贵的征服,就是征服了这 2020-07-03 …
求出下面每组数的最大公因数,并说一说他们的公因数还有哪些?回答正确加悬赏.(1)25和75最大公因 2020-07-31 …
一张试卷给出一段话,然后让考生去写,那么试卷给出的那段话用抄下去吗试卷为:_给出一段话:XXXXXX 2020-11-06 …
英语翻译当我做出人生最重要的决定时,聪明的你对我表现出突如其来的惊喜,在你心里我不是那个最好、最完美 2020-11-10 …
《书香蔬香》1.文章第一段在全文中起什么作用?2.文章以“书香蔬香”为题有什么好处?3.如何理解第三 2020-12-04 …
斜向上抛出物体,最高点速度和时间以初速度v0,抛射角向斜上方抛出一个物体,由抛出到经过最高点的时间是 2021-01-12 …