早教吧作业答案频道 -->数学-->
如图,已知O是△ABC的外接圆,AD是O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.(1)求证:BE是O的切线;(2)若BC=3,AC=5,求圆的直径AD及切线BE的长.
题目详情
如图,已知 O是△ABC的外接圆,AD是 O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.
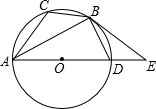
(1)求证:BE是 O的切线;
(2)若BC=
,AC=5,求圆的直径AD及切线BE的长.

(1)求证:BE是 O的切线;
(2)若BC=
| 3 |
▼优质解答
答案和解析
如图,
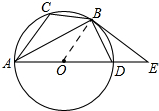
连接OB,∵BD=BC,
∴∠CAB=∠BAD,
∵∠EBD=∠CAB,
∴∠BAD=∠EBD,
∵AD是 O的直径,
∴∠ABD=90°,OA=BO,
∴∠BAD=∠ABO,
∴∠EBD=∠ABO,
∴∠OBE=∠EBD+∠OBD=∠ABD+∠OBD=∠ABD=90°,
∵点B在 O上,
∴BE是 O的切线,
(2)如图2,
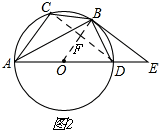
设圆的半径为R,连接CD,
∵AD为 O的直径,
∴∠ACD=90°,
∵BC=BD,
∴OB⊥CD,
∴OB∥AC,
∵OA=OD,
∴OF=
AC=
,
∵四边形ACBD是圆内接四边形,
∴∠BDE=∠ACB,
∵∠DBE=∠ACB,
∴△DBE∽△CAB,
∴
=
,
∴
=
,
∴DE=
,
∵∠OBE=∠OFD=90°,
∴DF∥BE,
∴
=
,
∴
=
,
∵R>0,
∴R=3,
∴AB=
=
∵
=
,
∴BE=
.

连接OB,∵BD=BC,
∴∠CAB=∠BAD,
∵∠EBD=∠CAB,
∴∠BAD=∠EBD,
∵AD是 O的直径,
∴∠ABD=90°,OA=BO,
∴∠BAD=∠ABO,
∴∠EBD=∠ABO,
∴∠OBE=∠EBD+∠OBD=∠ABD+∠OBD=∠ABD=90°,
∵点B在 O上,
∴BE是 O的切线,
(2)如图2,

设圆的半径为R,连接CD,
∵AD为 O的直径,
∴∠ACD=90°,
∵BC=BD,
∴OB⊥CD,
∴OB∥AC,
∵OA=OD,
∴OF=
| 1 |
| 2 |
| 5 |
| 2 |
∵四边形ACBD是圆内接四边形,
∴∠BDE=∠ACB,
∵∠DBE=∠ACB,
∴△DBE∽△CAB,
∴
| DB |
| AC |
| DE |
| BC |
∴
| ||
| 5 |
| DE | ||
|
∴DE=
| 3 |
| 5 |
∵∠OBE=∠OFD=90°,
∴DF∥BE,
∴
| OF |
| OB |
| OD |
| OE |
∴
| ||
| R |
| R | ||
R+
|
∵R>0,
∴R=3,
∴AB=
| AB2-BD2 |
| 33 |
∵
| AC |
| AB |
| BD |
| BE |
∴BE=
3
| ||
| 5 |
看了 如图,已知O是△ABC的外接...的网友还看了以下:
一次函数y=kx+b的图像与反比例函数y=m/x的图像交于a(2,1).b(-1,n)两点.(1) 2020-04-08 …
同比增长问题如果已知2010年某产品出口额为A元,同比增长B%.要求2010年这个产品比上年同期增 2020-05-22 …
an为等差数列,bn为等比数列,若a1=b1,a(2n+1)=b(2n+1),比较a(n+1),b 2020-06-03 …
直线ax-y+2=0与连接A(-3,1),B(-1,4)的线段相交,则a的取值范围?结果为-2≤a 2020-06-15 …
1.在绝缘板上方有一个不带电的金箔验电器A和一个带正电荷的空腔导体B,下列实验方法中能使验电器薄片 2020-06-18 …
一个正三棱柱恰好有一个内切球(即恰好与两底面和三个侧面都相切)和一外接球(即恰好经过三棱柱的6个顶 2020-07-14 …
已知a>b>c,求证1/a-c+1/b-c=4/a-c有没有更直接的证明方式 2020-07-20 …
问一道数学二次根式题.a=(√3)+(√7)b=(√3)-(√7)求[(a^2)^-1]+[(b^2 2020-11-25 …
一项工程,A独做需要9小时,B需要做12小时,如果A做1小时,然后B接替A做1小时,再由A接替B做1 2020-11-30 …
如图所示,A为导线,B、C为两根相同的电阻丝,当滑片P向左移动时,要使灯泡L的亮度不变,则开关S应( 2020-12-20 …