早教吧作业答案频道 -->数学-->
已知A(0,2),B(4,0).(1)如图1,连接AB,若D(0,-6),DE⊥AB于点E,B、C关于y轴对称,M是线段DE上的一点,且DM=AB,连接AM,试判断线段AC与AM之间的位置和数量关系,并证明你的结论
题目详情
已知A(0,2),B(4,0).
(1)如图1,连接AB,若D(0,-6),DE⊥AB于点E,B、C关于y轴对称,M是线段DE上的一点,且DM=AB,连接AM,试判断线段AC与AM之间的位置和数量关系,并证明你的结论;
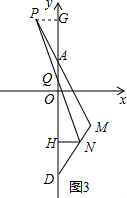
(2)如图2,在(1)的条件下,若N是线段DM上的一个动点,P是MA延长线上的一点,且DN=AP,连接PN交y轴于点Q,过点N作NH⊥y轴于点H,当N点在线段DM上运动时,△MQH的面积是否为定值?若是,请求出这个值;若不是,请说明理由.
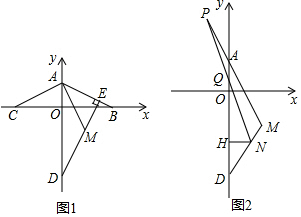
(1)如图1,连接AB,若D(0,-6),DE⊥AB于点E,B、C关于y轴对称,M是线段DE上的一点,且DM=AB,连接AM,试判断线段AC与AM之间的位置和数量关系,并证明你的结论;
(2)如图2,在(1)的条件下,若N是线段DM上的一个动点,P是MA延长线上的一点,且DN=AP,连接PN交y轴于点Q,过点N作NH⊥y轴于点H,当N点在线段DM上运动时,△MQH的面积是否为定值?若是,请求出这个值;若不是,请说明理由.

▼优质解答
答案和解析
(1)结论:AC=AM,AC⊥AM.理由如下:
∵A(0,2),B(4,0)D(0,-6),
∴OA=2,OD=6,OB=4,
∵AD=OA+OD=8,BC=2OB=8,
∴AD=BC,
在△CAB与△AMD中,
,
∴△CAB≌△AMD,
∴AC=AM,∠ACO=∠MAD,
∵∠ACO+∠CAO=90°,
∴∠MAD+∠CAO=∠MAC=90°,
∴AC=AM,AC⊥AM;
(2)是定值,定值为4.理由如下:
过P作PG⊥y轴于G,
在△PAG与△HND中,
,
∴△PAG≌△HND,
∴PG=HN,AG=HD,
∴AD=GH=8,
在△PQG与△NHQ中,
,
∴△PQG≌△NHQ,
∴QG=QH=
GH=4,
∴S△MQH=
×4×2=4.
∵A(0,2),B(4,0)D(0,-6),
∴OA=2,OD=6,OB=4,
∵AD=OA+OD=8,BC=2OB=8,
∴AD=BC,
在△CAB与△AMD中,
|
∴△CAB≌△AMD,
∴AC=AM,∠ACO=∠MAD,
∵∠ACO+∠CAO=90°,
∴∠MAD+∠CAO=∠MAC=90°,
∴AC=AM,AC⊥AM;

(2)是定值,定值为4.理由如下:
过P作PG⊥y轴于G,
在△PAG与△HND中,
|
∴△PAG≌△HND,
∴PG=HN,AG=HD,
∴AD=GH=8,
在△PQG与△NHQ中,
|
∴△PQG≌△NHQ,
∴QG=QH=
| 1 |
| 2 |
∴S△MQH=
| 1 |
| 2 |
看了 已知A(0,2),B(4,0...的网友还看了以下:
如图所示为氢原子能级图,下列说法正确的是()A.玻尔理论也能很好地解释复杂原子的光谱B.玻尔理论认 2020-05-14 …
如图所示为氢原子能级图,下列说法正确的是()A.玻尔理论也能很好地解释复杂原子的光谱B.玻尔理论认 2020-05-14 …
如图所示为氢原子能级图,下列说法正确的是()A.玻尔理论也能很好地解释复杂原子的光谱B.玻尔理论认 2020-05-14 …
数学题进来帮下1设函数f(x)={上面是x+1,x≤0下面是a,x>0,在点x=0处连续,则a=2 2020-07-15 …
已知:如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D, 2020-07-27 …
如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点 2020-07-27 …
醚键中两边的C上连的必须是三个单键吗?连一个单键和一个双键不可以吗?(就是说如果连了双键的话,还算不 2020-11-03 …
刑法问题:屠某非法侵入他人住宅后盗窃了5000元人民币,对屠某()。A.以非法侵入他人住宅罪论处B. 2020-11-06 …
氢叠氮酸中连氢的氮为何是sp2杂化根据价层电子对互斥理论,连氢的氮应是sp3杂化. 2020-12-01 …
英语翻译大连市副市长在”城市节约用水国际讨论会”上的欢迎词各位代表、女士们、先生们、朋友们:首先,我 2020-12-23 …