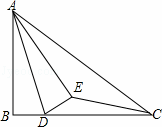
如图，已知在Rt△ABC中，∠ABC=90°，AB=6，BC=8，点D是边BC上的任意一点，以AD为折痕翻折△ABD，使点B落在点E处，连接EC，当△DEC为直角三角形时，BD的长为．

Question

如图，已知在Rt△ABC中，∠ABC=90°，AB=6，BC=8，点D是边BC上的任意一点，以AD为折痕翻折△ABD，使点B落在点E处，连接EC，当△DEC为直角三角形时，BD的长为 　　 ．

Answer 1

3或6
考点：
翻折变换（折叠问题）． 
分析：
在Rt△ABC中，∠ABC=90°，AB=6，BC=8，根据勾股定理求得AB==10，根据翻折的性质得AE=AB=6，DE=BD，∠AED=∠B=90°．①如图1，当∠DEC=90°时，推出点E在线段AC上，设BD=DE=x，则CD=8﹣x，根据勾股定理即可得到结果；②如图2，当∠EDC=90，于是得到∠BDE=90°，求得∠BDA=∠ADE=45°，于是得到△ABD是等腰直角三角形于是得到结果．

在Rt△ABC中，∠ABC=90°，AB=6，BC=8， ∴AB==10， ∵△AED是△ABD以AD为折痕翻折得到的， ∴AE=AB=6，DE=BD，∠AED=∠B=90°． 当△DEC为直角三角形， ①如图1，当∠DEC=90°时， ∵∠AED+∠DEC=180°， ∴点E在线段AC上， 设BD=DE=x，则CD=8﹣x， ∴CE=AB﹣AE=4， ∴DE2+CE2=CD2， 即x2+42=（8﹣x）2， 解得：x=3， ②如图2，当∠EDC=90， ∴∠BDE=90°， ∵∠BDA=∠ADE， ∴∠BDA=∠ADE=45°， ∴∠BAD=45°， ∴AB=BD=6． 综上所述：当△DEC为直角三角形时，BD的长为3或6． 故答案为：3或6．