早教吧作业答案频道 -->数学-->
如图,点B在线段AC上,点D、E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.(1)求证:AC=AD+CE;(2)若AD=3,CE=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q.若点P与A、B两点不重合,
题目详情
如图,点B在线段AC上,点D、E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.
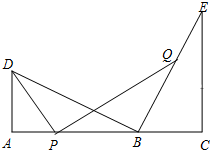
(1)求证:AC=AD+CE;
(2)若AD=3,CE=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q.若点P与A、B两点不重合,求
的值.

(1)求证:AC=AD+CE;
(2)若AD=3,CE=5,点P为线段AB上的动点,连接DP,作PQ⊥DP,交直线BE于点Q.若点P与A、B两点不重合,求
| DP |
| PQ |
▼优质解答
答案和解析
(1)∵BD⊥BE,
∴∠1+∠2=180°-90°=90°,
∵∠C=90°,
∴∠2+∠E=180°-90°=90°,
∴∠1=∠E,
∵在△ABD和△CEB中,
,
∴△ABD≌△CEB(AAS),
∴AB=CE,
∴AC=AB+BC=AD+CE;
(2)如图,过点Q作QF⊥BC于F,
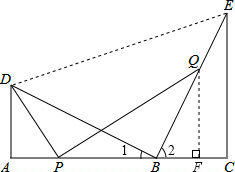
则△BFQ∽△BCE,
∴
=
,
即
=
,
∴QF=
BF,
∵DP⊥PQ,
∴∠APD+∠FPQ=180°-90°=90°,
∵∠APD+∠ADP=180°-90°=90°,
∴∠ADP=∠FPQ,
又∵∠A=∠PFQ=90°,
∴△ADP∽△FPQ,
∴
=
,
即
=
,
∴5AP-AP2+AP•BF=3•
BF,
整理得,(AP-BF)(AP-5)=0,
∵点P与A,B两点不重合,
∴AP≠5,
∴AP=BF,
由△ADP∽△FPQ得,
=
,
∴
=
.
∴∠1+∠2=180°-90°=90°,
∵∠C=90°,
∴∠2+∠E=180°-90°=90°,
∴∠1=∠E,
∵在△ABD和△CEB中,
|
∴△ABD≌△CEB(AAS),
∴AB=CE,
∴AC=AB+BC=AD+CE;
(2)如图,过点Q作QF⊥BC于F,

则△BFQ∽△BCE,
∴
| BF |
| BC |
| QF |
| CE |
即
| BF |
| 3 |
| QF |
| 5 |
∴QF=
| 5 |
| 3 |
∵DP⊥PQ,
∴∠APD+∠FPQ=180°-90°=90°,
∵∠APD+∠ADP=180°-90°=90°,
∴∠ADP=∠FPQ,
又∵∠A=∠PFQ=90°,
∴△ADP∽△FPQ,
∴
| AD |
| PF |
| AP |
| QF |
即
| 3 |
| 5-AP+BF |
| AP |
| QF |
∴5AP-AP2+AP•BF=3•
| 5 |
| 3 |
整理得,(AP-BF)(AP-5)=0,
∵点P与A,B两点不重合,
∴AP≠5,
∴AP=BF,
由△ADP∽△FPQ得,
| DP |
| PQ |
| AP |
| QF |
∴
| DP |
| PQ |
| 3 |
| 5 |
看了 如图,点B在线段AC上,点D...的网友还看了以下:
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
如果括号前面是加号,加上括号后,括号里面各项不变号如果括号前面是减号,加上括号后,括号里面各项要变 2020-04-25 …
化简a^2(x-b)(x-c)/(a-b)(a-c)+b^2(x-c)(x-a)/(b-c)(b- 2020-05-14 …
速求:ac(a+c)(a-c)+ba(b+a)(b-a)+cb(c+b)(c-b)怎样化为a^3( 2020-06-03 …
已知a+b+c=0,试求a^2/(2a^2+bc)+b^2/(2b^2+ac)+c^2/(2c^2 2020-06-11 …
设a,b,c∈R,证明a^2acc^23b(abc)≥0,并指出等号何时成立问题补充:证明:不妨设 2020-06-23 …
利用(a+b+c)^2=a^2+b^2^c^2+2ab+2ac+abc,推导(a+b+c)^2+a 2020-07-30 …
(a+b+c)^3-(b+c-a)^3-(c+a-b)^3-(a+b-c)^3=[(a+b+c)^ 2020-08-02 …
(1)1-100x=(1+10x)(1-10x)(2)-0.16+ab=(ab)-0(1)1-100 2020-10-31 …
已知a、b、c满足a<b<c,ab+bc+ac=0,abc=1,则()A.|a+b|>|c|B.|a 2020-11-01 …