早教吧作业答案频道 -->数学-->
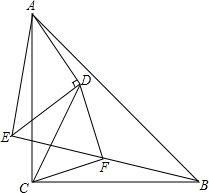
如图,△ACB与△ADE都是等腰直角三角形,∠ADE=∠ACB=90°,∠CDF=45°,DF交BE于F,求证:∠CFD=90°.
题目详情
如图,△ACB与△ADE都是等腰直角三角形,∠ADE=∠ACB=90°,∠CDF=45°,DF交BE于F,求证:∠CFD=90°.

▼优质解答
答案和解析
证明: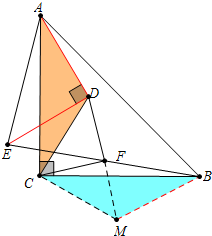 如图作CM⊥CD交DF的延长线于M,连接BM.
如图作CM⊥CD交DF的延长线于M,连接BM.
∵∠DCM=90°,∠CDM=45°,
∴∠CMD=90°-∠CDM=45°,
∴∠CDM=∠CMD=45°,
∴CD=CM,
∵∠ACB=∠DCM=90°,
∴∠ACD=∠MCB,
在△ACD和△BCM中,
,
∴△ACD≌△BCM,
∴AD=BM=ED,∠ADC=∠CMB,
∵∠BMF=∠CMB-∠CMD=∠CMB-45°,∠EDF=∠ADF-∠ADE=∠ADC+∠CDF-∠ADE=∠ADC-45°,
∴∠EDF=∠BMF,
在△EDF和△BMF中,
,
∴△EDF≌△BMF,
∴DF=FM,
∵CD=CM,
∴CF⊥DM,
∴∠CFD=90°.
 如图作CM⊥CD交DF的延长线于M,连接BM.
如图作CM⊥CD交DF的延长线于M,连接BM.∵∠DCM=90°,∠CDM=45°,
∴∠CMD=90°-∠CDM=45°,
∴∠CDM=∠CMD=45°,
∴CD=CM,
∵∠ACB=∠DCM=90°,
∴∠ACD=∠MCB,
在△ACD和△BCM中,
|
∴△ACD≌△BCM,
∴AD=BM=ED,∠ADC=∠CMB,
∵∠BMF=∠CMB-∠CMD=∠CMB-45°,∠EDF=∠ADF-∠ADE=∠ADC+∠CDF-∠ADE=∠ADC-45°,
∴∠EDF=∠BMF,
在△EDF和△BMF中,
|
∴△EDF≌△BMF,
∴DF=FM,
∵CD=CM,
∴CF⊥DM,
∴∠CFD=90°.
看了 如图,△ACB与△ADE都是...的网友还看了以下:
matlab求微分方程,常数项比如y=dsolve("Du=((a-u-b)*e-u*d)/(e* 2020-05-14 …
main(){unionEXAMPLE{struct{intx,y;}in;inta,b;}e;e 2020-06-12 …
(2011•太原)如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.AF平分∠C 2020-06-12 …
如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.AF平分∠CAB,交CD于点E 2020-06-13 …
用以下英文宇母填在上a,a,a,a,a,a,b,e,e,d,e,e,e,e,e,e,f,g,g用以 2020-06-24 …
设一数列a,b,c,d,e,f,通过栈结构不可能不可能排成的顺序数列为()A)c,b,e,f,d, 2020-06-28 …
五元一次方程的解法0.01349/[e+0.6842(1-e)]=a0.8638/[e+0.565 2020-07-16 …
(2014•贵阳)如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD 2020-11-13 …
多元一次方程求解a=0.1072(a+b+c+d+e)b=0.041(a+b+c+d+e)c=0.2 2020-12-14 …
有一张矩形纸片ABCD,AB=根号3,AD=根号2,将纸片折叠,使点D落在AB边上的点D'处,折痕为 2020-12-21 …