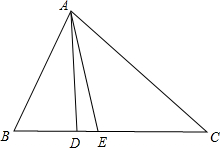
在△ABC中，∠BAC=75°，AB=3，AC=4，若点D，E都在边BC上，并且∠BAD=∠CAE=30°，则BD•BECD•CE=（）A.64B.34C.916D.2

Question

在△ABC中，∠BAC=75°，AB=3，AC=4，若点D，E都在边BC上，并且∠BAD=∠CAE=30°，则

(BD•BE)/(CD•CE)=（　　）

A.

(√(6))/(4)

B.

(3)/(4)

C.

(9)/(16)

D.

√(2)

Answer 1

如图，
由正弦定理得，(BD)/((1)/(2))=(3)/(sin∠BDA)①，(BE)/(sin35°)=(3)/(sin∠AEB)②，(CE)/((1)/(2))=(4)/(sin∠AEB)③，(CD)/(sin35°)=(4)/(sin∠BDA)④；
∴(①)/(④)•(②)/(③)得：(2sin35°•BD)/(CD)•(BE)/(2sin35°•CE)=(3)/(4)•(3)/(4)；
∴(BD•BE)/(CD•CE)=(9)/(16)．
故选C．