早教吧作业答案频道 -->数学-->
如图,△ABC中,∠ABC=60°,点E在边BC上,且EA=EB.(1)请先利用尺规作图的方法找到点E,在图A中标出(保留作图痕迹),在判断此时△ABC的形状(直接写出答案);(2)在图A中,取AE的中
题目详情
如图,△ABC中,∠ABC=60°,点E在边BC上,且EA=EB.
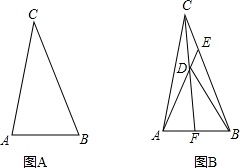
(1)请先利用尺规作图的方法找到点E,在图A中标出(保留作图痕迹),在判断此时△ABC的形状(直接写出答案);
(2)在图A中,取AE的中点D,若AD=CE,连接CD并延长交AB于点F,请先画出图形,再求∠CFA的度数;
(3)若∠ABC的大小不变,改变∠CAB的大小,得到图B,将(2)中“点D是AE的中点”改为“点D是AE上一点”,其他条件不变,猜想∠CFA与∠DBC的关系,并证明.

(1)请先利用尺规作图的方法找到点E,在图A中标出(保留作图痕迹),在判断此时△ABC的形状(直接写出答案);
(2)在图A中,取AE的中点D,若AD=CE,连接CD并延长交AB于点F,请先画出图形,再求∠CFA的度数;
(3)若∠ABC的大小不变,改变∠CAB的大小,得到图B,将(2)中“点D是AE的中点”改为“点D是AE上一点”,其他条件不变,猜想∠CFA与∠DBC的关系,并证明.
▼优质解答
答案和解析
(1)如图A,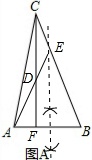
△AEC为等边三角形;
(2)如图A,∵AD=DE,AD=CE,
∴DE=CE,
∴∠ECD=∠EDC,
而∠AEB=∠ECD+∠EDC=60°,
∴∠ECD=30°,
∴∠CFA=∠B+∠BCF=60°+30°=90°;
(3)∠CFA-∠DBC=60°.理由如下:
作DM∥BC交AB于M,如图B,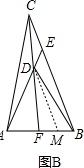
∵△ABE是等边三角形,
∴∠AMD=60°,AD=DM=AM,
∴∴△DAM是等边三角形,
∴∠DEC=∠BMD=120°,
∵DE=AE-AD,BM=AB-AM,
∴DE=BM,
在△DBM和△CDE中,
,
∴△DBM≌△CDE,
∴∠BDM=∠ECD,
∵DM∥BC,
∴∠BDM=∠CBD,
∴∠CBD=∠BCF,
∵∠CFA=∠ABC+∠BCF=60°+∠BCF,
∴∠CFA=60°+∠DBC,
即∠CFA-∠DBC=60°.

△AEC为等边三角形;
(2)如图A,∵AD=DE,AD=CE,
∴DE=CE,
∴∠ECD=∠EDC,
而∠AEB=∠ECD+∠EDC=60°,
∴∠ECD=30°,
∴∠CFA=∠B+∠BCF=60°+30°=90°;
(3)∠CFA-∠DBC=60°.理由如下:
作DM∥BC交AB于M,如图B,

∵△ABE是等边三角形,
∴∠AMD=60°,AD=DM=AM,
∴∴△DAM是等边三角形,
∴∠DEC=∠BMD=120°,
∵DE=AE-AD,BM=AB-AM,
∴DE=BM,
在△DBM和△CDE中,
|
∴△DBM≌△CDE,
∴∠BDM=∠ECD,
∵DM∥BC,
∴∠BDM=∠CBD,
∴∠CBD=∠BCF,
∵∠CFA=∠ABC+∠BCF=60°+∠BCF,
∴∠CFA=60°+∠DBC,
即∠CFA-∠DBC=60°.
看了 如图,△ABC中,∠ABC=...的网友还看了以下:
模仿句子单纯决不是幼稚的同义语.幼稚是童气未脱的胎迹,单纯是童年留下的财富.请保留一份单纯,使你多 2020-06-19 …
下列关于担保中留置的说法,正确的是( )。A.留置权人不占有留置财产B.留置财产只能是不 2020-06-27 …
如图所示,A同学通过平面镜可以看到隔墙的B同学(含眼睛),图中A、B同学用黑点代表.(1)请在图中 2020-07-22 …
在直线m上找出满足下列条件的点P.请保留作图痕迹,其中第(2)小题用尺规作图.(1)点P到A、B距 2020-08-02 …
中文语法请问有没有“a对b”留下深刻的印象这种说法?如果有,那么是a心里有b还是b心里有a? 2020-10-30 …
请为某中学学生餐厅拟一句标语,最恰当的是[]A.珍惜我,就是孝敬父母B.节约一粒米,留下黄金屋。C. 2020-11-02 …
下面在不同场合使用的敬辞或谦语不恰当的一项是()A.邀请朋友到家中做客,你可以说:“我在家里恭候您的 2020-11-10 …
按要求作图(请保留作图痕迹):(1)如图甲所示,小华用笤帚在扫地,O为支点,作用在A点的动力为F1, 2020-11-21 …
按照题目要求作图:(1)如图a所示为某同学用扫把扫地的示意图,请在图中扫把上画出动力F示意图及其相应 2020-11-21 …
仿句几句,给50分1.单纯绝不是幼稚的同义词.幼稚是童气未脱的胎迹,单纯是童年留下的财富.这个仿1句 2020-11-26 …