早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠ABC=60°,∠C=45°,AD是BC边上的高,∠ABC的角平分线BE交AD于点F,则图中共有等腰三角形()A、2个B、3个C、4个D、5个
题目详情
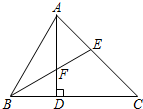 如图,在△ABC中,∠ABC=60°,∠C=45°,AD是BC边上的高,∠ABC的角平分线BE交AD于点F,则图中共有等腰三角形( )
如图,在△ABC中,∠ABC=60°,∠C=45°,AD是BC边上的高,∠ABC的角平分线BE交AD于点F,则图中共有等腰三角形( )| A、2个 | B、3个 | C、4个 | D、5个 |
▼优质解答
答案和解析
考点:
等腰三角形的判定
专题:
分析:
根据在△ABC中,∠ABC=60°,∠ACB=45°,利用三角形内角和定理求得∠BAC=75°,然后可得等腰三角形.
(1)∵∠ABC=60°,∠ACB=45°,AD是高,∴∠DAC=45°,∴CD=AD,∴△ADC为等腰直角三角形,∵∠ABC=60°,BE是∠ABC平分线,∴∠ABE=∠CBE=30°,在△ABD中,∠BAD=180°-∠ABD-∠ADB=180°-60°-90°=30°,∴∠ABF=∠BAD=30°,∴AF=BF即△ABF是等腰三角形,在△ABC中,∠BAC=180°-∠ABC-∠ACB=180°-60°-45°=75°,∵∠AEB=∠CBE+∠ACB=30°+45°=75°,∴∠BAE=∠BEA,∴AB=EB即△ABE是等腰三角形,∴等腰三角形有△ACD,△ABF,△ABE;故选B.
点评:
本题考查了三角形的内角和定理以及三角形的高、角平分线,等腰三角形的判定、等边三角形的判定,是基础知识要熟练掌握.
考点:
等腰三角形的判定
专题:
分析:
根据在△ABC中,∠ABC=60°,∠ACB=45°,利用三角形内角和定理求得∠BAC=75°,然后可得等腰三角形.
(1)∵∠ABC=60°,∠ACB=45°,AD是高,∴∠DAC=45°,∴CD=AD,∴△ADC为等腰直角三角形,∵∠ABC=60°,BE是∠ABC平分线,∴∠ABE=∠CBE=30°,在△ABD中,∠BAD=180°-∠ABD-∠ADB=180°-60°-90°=30°,∴∠ABF=∠BAD=30°,∴AF=BF即△ABF是等腰三角形,在△ABC中,∠BAC=180°-∠ABC-∠ACB=180°-60°-45°=75°,∵∠AEB=∠CBE+∠ACB=30°+45°=75°,∴∠BAE=∠BEA,∴AB=EB即△ABE是等腰三角形,∴等腰三角形有△ACD,△ABF,△ABE;故选B.
点评:
本题考查了三角形的内角和定理以及三角形的高、角平分线,等腰三角形的判定、等边三角形的判定,是基础知识要熟练掌握.
看了 如图,在△ABC中,∠ABC...的网友还看了以下:
a除以b商余2,如a和b都扩大100倍,那么商是()余数是() 2020-06-03 …
1.若2:(a-3)=(a-3):8,则a=2.如果线段a=2,且a,b的比例中项为根号10,那么 2020-06-03 …
某珠宝店被盗,警方已发现如下线索:(1)A、B、C三人至少有一个人是罪犯;(2)如A是罪犯,则B一定 2020-06-05 …
1.若a-1/a=4,则a^2+1/a^2=2.如果(3x+3y+1)(3x+3y-1)=35,那 2020-07-30 …
1.下列各式中,形如a^2±2ab+b^2形式的多项式有()①a^2-a+1/4②x^2+xy+y 2020-07-31 …
本问题分为如下两步:1、给出形如A(n+1)=pAn^2+qAn的递推公式和A1的值,求通项.例如 2020-08-01 …
在学习过程中,把公式进行变形,会有意想不到的新发现,如由(a+b)∧2=a∧2+2ab+b∧2变形 2020-08-02 …
绝对值小于派的整数有多少?补充题:1.已知A.B互为相反数,C.D互为倒数,M是绝对值等于2的数,求 2020-12-17 …
难题,比如齐次轮换对称式,双换元,双十字等等只要10道,只要是难题追加分!双十字-3x^2+4y^2 2020-12-24 …
假如有一个集合A={1,2,3},那么用描述法可以表示成如下形式吗?A={x|x=1,2,3}A={ 2021-01-13 …