早教吧作业答案频道 -->数学-->
如图,∠ABC=45°,△ADE是等腰直角三角形,AE=AD,顶点A、D分别在∠ABC的两边BA、BC上滑动(不与点B重合),△ADE的外接圆交BC于点F,点D在点F的右侧,O为圆心.(1)求证:△ABD≌△AFE(2)
题目详情
如图,∠ABC=45°,△ADE是等腰直角三角形,AE=AD,顶点A、D分别在∠ABC的两边BA、BC上滑动(不与点B重合),△ADE的外接圆交BC于点F,点D在点F的右侧,O为圆心.
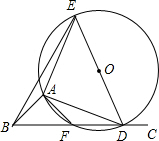
(1)求证:△ABD≌△AFE
(2)若AB=4
,8
<BE≤4
,求 O的面积S的取值范围.
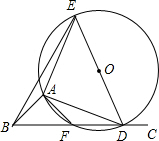
(1)求证:△ABD≌△AFE
(2)若AB=4
| 2 |
| 2 |
| 13 |
▼优质解答
答案和解析
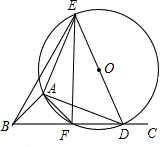 (1)∵△ADE是等腰直角三角形,AE=AD,
(1)∵△ADE是等腰直角三角形,AE=AD,
∴∠EAD=90°,∠AED=∠ADE=45°,
∵
=
,
∴∠ADE=∠AFE=45°,
∵∠ABD=45°,
∴∠ABD=∠AFE,
∵
=
,
∴∠AEF=∠ADB,
∵AF=AF,
∴△ABD≌△AFE;
(2)∵△ABD≌△AFE,
∴BD=EF,∠EAF=∠BAD,
∴∠BAF=∠EAD=90°,
∵AB=4
,
∴BF=
=
=8,
设BD=x,则EF=x,DF=x-8,
∵BE2=EF2+BF2,8
<BE≤4
,
∴128<EF2+82≤208,
∴8<EF≤12,即8<x≤12,
则S=
DE2=
[x2+(x-8)2]=
(x-4)2+8π,
∵
>0,
∴抛物线的开口向上,
又∵对称轴为直线x=4,
∴当8<x≤12时,S随x的增大而增大,
∴16π<S≤40π.
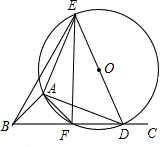 (1)∵△ADE是等腰直角三角形,AE=AD,
(1)∵△ADE是等腰直角三角形,AE=AD,∴∠EAD=90°,∠AED=∠ADE=45°,
∵
 |
| AE |
 |
| AE |
∴∠ADE=∠AFE=45°,
∵∠ABD=45°,
∴∠ABD=∠AFE,
∵
 |
| AF |
 |
| AF |
∴∠AEF=∠ADB,
∵AF=AF,
∴△ABD≌△AFE;
(2)∵△ABD≌△AFE,
∴BD=EF,∠EAF=∠BAD,
∴∠BAF=∠EAD=90°,
∵AB=4
| 2 |
∴BF=
| AB |
| cos∠ABF |
4
| ||
| cos45° |
设BD=x,则EF=x,DF=x-8,
∵BE2=EF2+BF2,8
| 2 |
| 13 |
∴128<EF2+82≤208,
∴8<EF≤12,即8<x≤12,
则S=
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
∵
| π |
| 2 |
∴抛物线的开口向上,
又∵对称轴为直线x=4,
∴当8<x≤12时,S随x的增大而增大,
∴16π<S≤40π.
看了 如图,∠ABC=45°,△A...的网友还看了以下:
气象台发布的卫星云图显示,某台风在海岛A北偏西60°方向上的B点处生成,城市C在海岛A北偏东45° 2020-05-16 …
抛物线y=x2+bx+c(b小于等于0)的图像与x轴交于A`B两点,与y轴交于C点,其中点A坐标为 2020-06-29 …
如图,在正方形ABCD中,E为直线AB上的动点(不与A,B重合),作射线DE并绕点D逆时针旋转45 2020-07-09 …
已知A、B是数轴上两点,A点对应数为12,B点对应数为42.(1)C是数轴上一点,且AC=2AB, 2020-07-21 …
已知A、B是数轴上两点,A点对应数为12,B点对应数为42.(1)C是数轴上一点,且AC=2AB, 2020-07-22 …
如图(甲)所示,A车原来临时停在一水平路面上,B车在后面匀速向A车靠近,A车司机发现后启动A车,以 2020-07-22 …
真空中Ox坐标轴上的某点有一个点电荷Q,坐标轴上A、B两点的坐标分别为0.2m和0.7m。在A点放 2020-07-31 …
如图所示,真空中Ox坐标轴上的某点有一个点电荷Q,坐标轴上A、B两点的坐标分别为0.2m和0.7m 2020-07-31 …
以A点后视点,以B点为架站点,测量C,D点.得出坐标,再以D点为架站点,A点为后视点,测量B,C点, 2021-01-02 …
将以篮球从地面上方B点斜向上抛出,将一篮球从地面上方B点斜向上抛出,刚好垂直击中篮板上A点,不计空气 2021-01-12 …