早教吧作业答案频道 -->数学-->
如图,△ABC内接于O,AC为O的直径,PB是O的切线,B为切点,OP⊥BC,垂足为E,交O于D,连接BD.(1)求证:BD平分∠PBC;(2)若O的半径为1,PD=3DE,求OE及AB的长.
题目详情
如图,△ABC内接于 O,AC为 O的直径,PB是 O的切线,B为切点,OP⊥BC,垂足为E,交 O于D,连接BD.
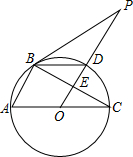
(1)求证:BD平分∠PBC;
(2)若 O的半径为1,PD=3DE,求OE及AB的长.

(1)求证:BD平分∠PBC;
(2)若 O的半径为1,PD=3DE,求OE及AB的长.
▼优质解答
答案和解析
(1)证明:连接OB.
∵PB是 O切线,
∴OB⊥PB,
∴∠PBO=90°,
∴∠PBD+∠OBD=90°,
∵OB=OD,
∴∠OBD=∠ODB,
∵OP⊥BC,
∴∠BED=90°,
∴∠DBE+∠BDE=90°,
∴∠PBD=∠EBD,
∴BD平分∠PBC.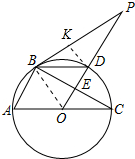
(2) 作DK⊥PB于K,
∵
=
=
,
∵BD平分∠PBE,DE⊥BE,DK⊥PB,
∴DK=DE,
∴
=
=
,
∵∠OBE+∠PBE=90°,∠PBE+∠P=90°,
∴∠OBE=∠P,∵∠OEB=∠BEP=90°,
∴△BEO∽△PEB,
∴
=
,
∴
=
=
,
∵BO=1,
∴OE=
,
∵OE⊥BC,
∴BE=EC,∵AO=OC,
∴AB=2OE=
.
∵PB是 O切线,
∴OB⊥PB,
∴∠PBO=90°,
∴∠PBD+∠OBD=90°,
∵OB=OD,
∴∠OBD=∠ODB,
∵OP⊥BC,
∴∠BED=90°,
∴∠DBE+∠BDE=90°,
∴∠PBD=∠EBD,
∴BD平分∠PBC.

(2) 作DK⊥PB于K,
∵
| S△BDE |
| S△BDP |
| ||
|
| DE |
| DP |
∵BD平分∠PBE,DE⊥BE,DK⊥PB,
∴DK=DE,
∴
| BE |
| PB |
| ED |
| PD |
| 1 |
| 3 |
∵∠OBE+∠PBE=90°,∠PBE+∠P=90°,
∴∠OBE=∠P,∵∠OEB=∠BEP=90°,
∴△BEO∽△PEB,
∴
| BO |
| PB |
| OE |
| BE |
∴
| OE |
| BO |
| BE |
| PB |
| 1 |
| 3 |
∵BO=1,
∴OE=
| 1 |
| 3 |
∵OE⊥BC,
∴BE=EC,∵AO=OC,
∴AB=2OE=
| 2 |
| 3 |
看了 如图,△ABC内接于O,AC...的网友还看了以下:
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
高一数学命题是假命题的是哪些(15日19:10:40)1、已知直线a,b,平面A,下列命题是假命题 2020-05-20 …
关于化学反应A+B=C+D,下列说法中正确的是:A.若C是单质,D为化合物,则A和B中一定有一种是 2020-06-06 …
若a,b,c,d,都是质数,切a的平方+b的平方+c的平方+d的平方=78,a的平方-b的平方=c 2020-07-09 …
如图所示,数轴上标出若干个点,每相邻两点相距一个单位长度,点A,B,C,D对应的数分别是整数a,b 2020-07-13 …
下列命题中,是真命题的是()A.两条直线被第三条直线所截,同位角相等B.若a⊥b,b⊥c则a⊥cC 2020-07-29 …
下列命题是真命题的是()A.垂直于同一条直线的两条直线互相平行B.同旁内角互补C.若a2=b2,则 2020-07-29 …
(2013•随州)如图是人体某处血管结构和血流方向示意图,下列有关叙述正确的是()A.若b为肾小球 2020-07-29 …
设平面内有四边形ABCD和点O,OA=a,OB=b,OC=c,OD=d,若a+c=b+d,试判断四 2020-08-01 …
下列推断正确的是a若│a│=│b│,则a=bb若│a│=b,则a=bc若a=负b,则|a|等于|b| 2020-12-28 …