如图，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE，BF交于点G，将△BCF沿BF对折，得到△BPF，延长FP交BA延长线于点Q，下列结论正确的个数是（）①AE=BF；②AE⊥BF；③sin∠BQP=45；④S

Question

如图，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE，BF交于点G，将△BCF沿BF对折，得到△BPF，延长FP交BA延长线于点Q，下列结论正确的个数是（　　）
①AE=BF；②AE⊥BF；③sin∠BQP=

(4)/(5)；④S_{四边形ECFG}=2S_△BGE．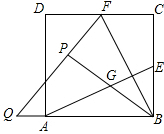

A. 4

B. 3

C. 2

D. 1

Answer 1

∵E，F分别是正方形ABCD边BC，CD的中点，
∴CF=BE，
在△ABE和△BCF中，

AB=BC

∠ABE=∠BCF

BE=CF

，
∴Rt△ABE≌Rt△BCF（SAS），
∴∠BAE=∠CBF，AE=BF，故①正确；
又∵∠BAE+∠BEA=90°，
∴∠CBF+∠BEA=90°，
∴∠BGE=90°，
∴AE⊥BF，故②正确；
根据题意得，FP=FC，∠PFB=∠BFC，∠FPB=90°
∵CD∥AB，
∴∠CFB=∠ABF，
∴∠ABF=∠PFB，
∴QF=QB，
令PF=k（k>0），则PB=2k
在Rt△BPQ中，设QB=x，
∴x²=（x-k）²+4k²，
∴x=(5k)/(2)，
∴sin=∠BQP=(BP)/(QB)=(4)/(5)，故③正确；
∵∠BGE=∠BCF，∠GBE=∠CBF，
∴△BGE∽△BCF，
∵BE=(1)/(2)BC，BF=(√(5))/(2)BC，
∴BE：BF=1：√(5)，
∴△BGE的面积：△BCF的面积=1：5，
∴S_{四边形ECFG}=4S_△BGE，故④错误．
故选：B．