早教吧作业答案频道 -->数学-->
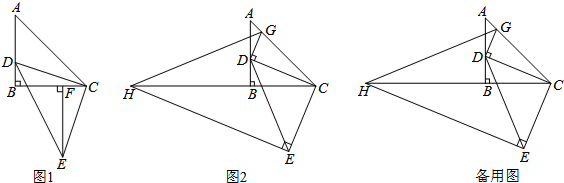
△ABC为等腰直角三角形,∠ABC=90°,点D在AB边上(不与点A、B重合),以CD为腰作等腰直角△CDE,∠DCE=90°.(1)如图1,作EF⊥BC于F,求证:△DBC≌△CFE;(2)在图1中,连接AE交BC于M,求ADBM
题目详情
△ABC为等腰直角三角形,∠ABC=90°,点D在AB边上(不与点A、B重合),以CD为腰作等腰直角△CDE,∠DCE=90°.
(1)如图1,作EF⊥BC于F,求证:△DBC≌△CFE;
(2)在图1中,连接AE交BC于M,求
的值;
(3)如图2,过点E作EH⊥CE交CB的延长线于点H,过点D作DG⊥DC,交AC于点G,连接GH.当点D在边AB上运动时,式子
的值会发生变化吗?若不变,求出该值;若变化请说明理由.
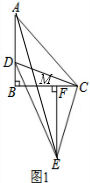
(1)如图1,作EF⊥BC于F,求证:△DBC≌△CFE;
(2)在图1中,连接AE交BC于M,求
| AD |
| BM |
(3)如图2,过点E作EH⊥CE交CB的延长线于点H,过点D作DG⊥DC,交AC于点G,连接GH.当点D在边AB上运动时,式子
| HE-GD |
| GH |

▼优质解答
答案和解析
 (1)证明:∵△CDE为等腰直角三角形,∠DCE=90°.
(1)证明:∵△CDE为等腰直角三角形,∠DCE=90°.
∴CD=CE,∠DCB+∠ECF=90°,
∵EF⊥BC,
∴∠ECF+∠CEF=90°,
∴∠DCB=∠CEF,
在△DBC和△CEF中,
,
∴△DBC≌△CFE;
(2) 如图1,
∵△DBC≌△CFE,
∴BD=CF,BC=EF,
∵△ABC为等腰直角三角形,
∴AB=BC,
∴AB=EF,AD=BF,
在△ABM和△EFM中,
,
∴△ABM≌△EFM,
∴BM=FM,
∴BF=2BM,
∴AD=2BM,
∴
的值为2;
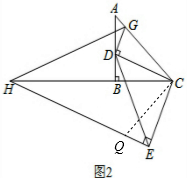 (3)
(3)
的值不变.
在EH上截取EQ=DG,如图2,
在△CDG和△CEQ中
,
∴△CDG≌△CEQ,
∴CG=CQ,∠DCG=∠ECQ,
∵∠DCG+∠DCB=45°,
∴∠ECQ+∠DCB=45°,
而∠DCE=90°,
∴∠HCQ=45°,
∴∠HCQ=∠HCG,
在△HCG和△HCQ中,
,
∴△HCG≌△HCQ,
∴HG=HQ,
∴
=
=
=1.
 (1)证明:∵△CDE为等腰直角三角形,∠DCE=90°.
(1)证明:∵△CDE为等腰直角三角形,∠DCE=90°.∴CD=CE,∠DCB+∠ECF=90°,
∵EF⊥BC,
∴∠ECF+∠CEF=90°,
∴∠DCB=∠CEF,
在△DBC和△CEF中,
|
∴△DBC≌△CFE;
(2) 如图1,
∵△DBC≌△CFE,
∴BD=CF,BC=EF,
∵△ABC为等腰直角三角形,
∴AB=BC,
∴AB=EF,AD=BF,
在△ABM和△EFM中,
|
∴△ABM≌△EFM,
∴BM=FM,
∴BF=2BM,
∴AD=2BM,
∴
| AD |
| BM |
 (3)
(3) | HE-GD |
| GH |
在EH上截取EQ=DG,如图2,
在△CDG和△CEQ中
|
∴△CDG≌△CEQ,
∴CG=CQ,∠DCG=∠ECQ,
∵∠DCG+∠DCB=45°,
∴∠ECQ+∠DCB=45°,
而∠DCE=90°,
∴∠HCQ=45°,
∴∠HCQ=∠HCG,
在△HCG和△HCQ中,
|
∴△HCG≌△HCQ,
∴HG=HQ,
∴
| HE-GD |
| GH |
| HQ+QE-GD |
| HG |
| HG+DG-GD |
| HG |
看了 △ABC为等腰直角三角形,∠...的网友还看了以下:
关于比例的基本性质已知a比b等于c比d(b+或-d不等于0),求证:a+c比a-c等于b+d比b- 2020-05-16 …
信托公司终止时,信托财产( )其清算财产。A.不属于B.属于C.等同于D.等于 2020-05-27 …
工作监护制度规定,监护人的安全技术等级应( )操作人。A: 低于B: 高于C: 等同于D: 稍低于 2020-05-29 …
人像摄影的人物表情是靠( )的。A.“摆”B.“抓”C.“等”D.“导” 2020-05-31 …
铸铁管的耐腐蚀性能()于碳素钢管。A.低B.优C.等D.不高 2020-05-31 …
a推出b推出c等价于d,a与d的关系是? 2020-06-03 …
初三比例式计算.如题.已知a/b=c/d(bd不等于0).判断下列比例式是否成立.并说明理由.a- 2020-06-10 …
逻辑推理题A推出B且C等价于什么推-A 2020-07-05 …
求证:已知a是非零向量,且b不等于c,证明a*b=a*c等价于a垂直(b-c) 2020-08-01 …
某省2016年高中数学学业水平测试的原始成绩采用百分制,发布成绩使用等级制,各等制划分标准如表所示: 2020-11-04 …