早教吧作业答案频道 -->数学-->
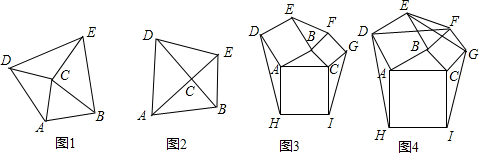
如图1,若分别以△ABC和AC、BC两边为直角边向外侧作等腰直角△ACD、△BCE,则称这两个等腰直角三角形为外展双叶等腰直角三角形.(1)发现:如图2,当∠ACB=90°,求证:△ABC与△DCE的面
题目详情
如图1,若分别以△ABC和AC、BC两边为直角边向外侧作等腰直角△ACD、△BCE,则称这两个等腰直角三角形为外展双叶等腰直角三角形.
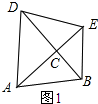
(1)发现:如图2,当∠ACB=90°,求证:△ABC与△DCE的面积相等.
(2)引申:如果∠ACB≠90°时.(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由.
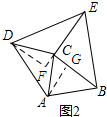
(3)运用:①如图3,分别以△ABC的三边为边向外侧作四边形ABED、BCFG和ACIH为正方形,则称这三个正方形为外展三叶正方形.已知△ABC中,AB=4,BC=3,当△ABC满足___时,图中△ADH、△BEF、△CGI的面积和有最大值是___②如图4,在△ADH、△BEF、△CGI的面积和取最大值时,试写出S△DEF、S△GFE、S正方形AHIC三者之间的数量关系.
(1)发现:如图2,当∠ACB=90°,求证:△ABC与△DCE的面积相等.
(2)引申:如果∠ACB≠90°时.(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由.
(3)运用:①如图3,分别以△ABC的三边为边向外侧作四边形ABED、BCFG和ACIH为正方形,则称这三个正方形为外展三叶正方形.已知△ABC中,AB=4,BC=3,当△ABC满足___时,图中△ADH、△BEF、△CGI的面积和有最大值是___②如图4,在△ADH、△BEF、△CGI的面积和取最大值时,试写出S△DEF、S△GFE、S正方形AHIC三者之间的数量关系.

▼优质解答
答案和解析
(1)如图1所示:
∵△ACD和△BCE均为等腰直角三角形,
∴DC=AC,CE=CB,∠ACD=∠BCE=90°.
∵∠ACB=∠ACD=∠BCE=90°,
∴∠DCE=90°.
在△DEC和△ABC中,
,
∴△DCE≌△ACB.
∴△ABC与△DCE的面积相等.
(2)成立.
理由:如图2所示:过点A作AG⊥BC,过点D作DF⊥CE,垂足为F.
∵△ACD和△BCE均为等腰直角三角形,
∴∠DCA=∠ECB=∠FCB=90°,DC=AC,CE=CB.
∵FE⊥BC,AG⊥CB,
∴FC∥AG.
∴∠FCA=∠GAC.
∵∠DCF+∠FCA=90°,∠FCA+∠ACG=90°,
∴∠DCF=∠ACG.
在△DCF和△ACG中,
,
∴△DCF≌△ACG.
∴FD=AG.
又∵CE=CB.
∴
CE•DC=
CB•AG,即△ABC与△DCE的面积相等.
(3)①如图3所示:
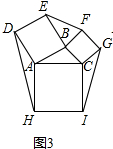
∵由(2)可知:S△ADH=S△ABC、S△BEF=S△ABC、S△CGI=S△ABC,
∴S△ADH+S△BEF+S△CGI=3S△ABC.
∴当∠ACB=90°,时S△ADH+S△BEF+S△CGI有最大值,最大值=3×
×3×4=18.
故答案为:∠ACB=90°;18.
②S△DEF+S△EFG=
S正方形AHIC.
理由:由①可知当∠ACB=90°时,S△ADH+S△BEF+S△CGI有最大值.
当∠ACB=90°时,如图4所示:
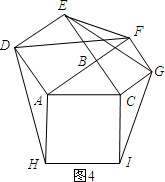
∵四边形ABED为正方形,
∴∠ABE=90°.
又∵∠ABC=90°,
∴∠ABE+∠ABC=90°+90°=180°.
∴点E、B、C在一条直线上.
∴△DEF的面积=
ED•AD=
AB2.
同理:△EFG的面积=
FG•CG=
CB2.
∵AC2=AB2+BC2,
∴S△DEF+S△EFG=
AB2+
CB2=
AC2=
S正方形AHIC.
∴S△DEF+S△EFG=
S正方形AHIC.

∵△ACD和△BCE均为等腰直角三角形,
∴DC=AC,CE=CB,∠ACD=∠BCE=90°.
∵∠ACB=∠ACD=∠BCE=90°,
∴∠DCE=90°.
在△DEC和△ABC中,
|
∴△DCE≌△ACB.
∴△ABC与△DCE的面积相等.
(2)成立.
理由:如图2所示:过点A作AG⊥BC,过点D作DF⊥CE,垂足为F.

∵△ACD和△BCE均为等腰直角三角形,
∴∠DCA=∠ECB=∠FCB=90°,DC=AC,CE=CB.
∵FE⊥BC,AG⊥CB,
∴FC∥AG.
∴∠FCA=∠GAC.
∵∠DCF+∠FCA=90°,∠FCA+∠ACG=90°,
∴∠DCF=∠ACG.
在△DCF和△ACG中,
|
∴△DCF≌△ACG.
∴FD=AG.
又∵CE=CB.
∴
| 1 |
| 2 |
| 1 |
| 2 |
(3)①如图3所示:

∵由(2)可知:S△ADH=S△ABC、S△BEF=S△ABC、S△CGI=S△ABC,
∴S△ADH+S△BEF+S△CGI=3S△ABC.
∴当∠ACB=90°,时S△ADH+S△BEF+S△CGI有最大值,最大值=3×
| 1 |
| 2 |
故答案为:∠ACB=90°;18.
②S△DEF+S△EFG=
| 1 |
| 2 |
理由:由①可知当∠ACB=90°时,S△ADH+S△BEF+S△CGI有最大值.
当∠ACB=90°时,如图4所示:

∵四边形ABED为正方形,
∴∠ABE=90°.
又∵∠ABC=90°,
∴∠ABE+∠ABC=90°+90°=180°.
∴点E、B、C在一条直线上.
∴△DEF的面积=
| 1 |
| 2 |
| 1 |
| 2 |
同理:△EFG的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∵AC2=AB2+BC2,
∴S△DEF+S△EFG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△DEF+S△EFG=
| 1 |
| 2 |
看了 如图1,若分别以△ABC和A...的网友还看了以下:
下列关于频率分布直方图的说法,正确的是[]A.直方图的高表示取某数的频率B.直方图的高表示该组上的 2020-04-08 …
下列哪些统计图适用于计数资料A.直条图、直方图B.线图、半对数线图C.直条图、百分直条图D.百分直条 2020-06-07 …
利用斜二测画法得到的:①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图 2020-06-20 …
利用斜二测画法得到的:①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图 2020-06-27 …
关于斜二测画法画直观图说法不正确的是()A.在实物图中取坐标系不同,所得的直观图有可能不同B.平行 2020-06-27 …
关于斜二测画法画直观图说法不正确的是()A.在实物图中取坐标系不同,所得的直观图有可能不同B.平行 2020-06-27 …
直方图与条形图的差别下列关于直方图与条形图差别的说法中,不正确的是?A.条形图用于展示分类数据,直 2020-07-29 …
关于样本频率分布直方图与总体密度曲线的关系,下列说法中正确的是A.频率分布直方图与总体密度曲线无关 2020-07-29 …
4、下列说法正确的是()A水平放置的正方形的直观图可能是梯形B两条相交直线的直观图可能是平行直线C 2020-08-01 …
1图在直三棱柱AB小-A图B图小图中,∠A小B=20°,AA图=2,A小=B小=图&nbpp;则异 2020-08-02 …