早教吧作业答案频道 -->数学-->
已知:如图,△ABC中,AD平分∠BAC交BC于点D,且∠ADC=60°,若∠ACB为钝角,且AB>AC,BD>DC.(1)求证:BD-DC<AB-AC;(2)若点E在AD上,且DE=DB,延长CE交AB于点F,求∠BFC的度数.
题目详情
已知:如图,△ABC中,AD平分∠BAC交BC于点D,且∠ADC=60°,若∠ACB为钝角,且AB>AC,BD>DC.
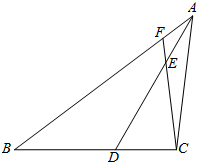
(1)求证:BD-DC<AB-AC;
(2)若点E在AD上,且DE=DB,延长CE交AB于点F,求∠BFC的度数.

(1)求证:BD-DC<AB-AC;
(2)若点E在AD上,且DE=DB,延长CE交AB于点F,求∠BFC的度数.
▼优质解答
答案和解析
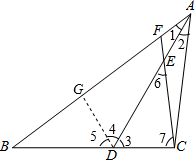 (1)证明:在AB上截取AG,使AG=AC,连接GD.(如图)
(1)证明:在AB上截取AG,使AG=AC,连接GD.(如图)
∵AD平分∠BAC,
∴∠1=∠2.
在△AGD和△ACD中,
,
∴△AGD≌△ACD(SAS).
∴DG=DC.
∵△BGD中,BD-DG<BG,
∴BD-DC<BG.
∵BG=AB-AG=AB-AC,
∴BD-DC<AB-AC;
(2) ∵由(1)知△AGD≌△ACD,
∴GD=CD,∠4=∠3=60°.
∴∠5=180°-∠3-∠4=180°-60°-60°=60°.
∴∠5=∠3.
在△BGD和△ECD中,
,
∴△BGD≌△ECD(SAS).
∴∠B=∠6.
∵△BFC中,∠BFC=180°-∠B-∠7=180°-∠6-∠7=∠3,
∴∠BFC=60°.
 (1)证明:在AB上截取AG,使AG=AC,连接GD.(如图)
(1)证明:在AB上截取AG,使AG=AC,连接GD.(如图)∵AD平分∠BAC,
∴∠1=∠2.
在△AGD和△ACD中,
|
∴△AGD≌△ACD(SAS).
∴DG=DC.
∵△BGD中,BD-DG<BG,
∴BD-DC<BG.
∵BG=AB-AG=AB-AC,
∴BD-DC<AB-AC;
(2) ∵由(1)知△AGD≌△ACD,
∴GD=CD,∠4=∠3=60°.
∴∠5=180°-∠3-∠4=180°-60°-60°=60°.
∴∠5=∠3.
在△BGD和△ECD中,
|
∴△BGD≌△ECD(SAS).
∴∠B=∠6.
∵△BFC中,∠BFC=180°-∠B-∠7=180°-∠6-∠7=∠3,
∴∠BFC=60°.
看了 已知:如图,△ABC中,AD...的网友还看了以下:
若a+b=b+c,则a-b(c为整式)若a=b,则ac=bc(c为整式)若ac=bc,则a=b(c 2020-04-22 …
化简下列逻辑函数①F=(A+B)C+AB②F=AC+AB+BC③F=ABC+ABC+ABC+ABC 2020-04-25 …
由a=b一定可以得出的等式是()A.a÷c=b÷c由a=b一定可以得出的等式是()A.a÷c=b÷ 2020-06-06 …
求解一题证明题!高数设f(x)与g(x)在[a,b]上连续,在(a,b)上可导,f(a)=f(b) 2020-08-01 …
一道关于导数的问题!已知函数f(x)=x^2+bx+c(b,c∈R),对任意的X∈R,恒有f(x) 2020-08-03 …
EXCEL循环或计算问题。F=A+B+C+D+E。(A.B.C.D.E.F.均要大于零)E=A*10 2020-11-01 …
100%收购公司其中一名法人股东涉及到的问题事实:A.B.C.D为四个法人。A.B公司为C公司的股东 2020-11-06 …
如图三条曲线表示C、Si和P元素的四级电离能变化趋势.下列说法正确的是()A.电负性:c>b>aB. 2020-11-11 …
在三角形ABC和三角形A'B'C'中CD,C'D'分别是高,并且AC=A'C;,CD=C'D',∠A 2020-11-28 …
在一个4变量逻辑函数F(A,B,C,D)中,子项AD意味着包含了的多少个最小项在一个4变量逻辑函数F 2020-12-08 …