早教吧作业答案频道 -->数学-->
是否存在常数a、b、c使得等式1×22+2×32+3×42+…+n(n+1)2=(an2+bn+c)对一切正整数n都成立?并证明你的结论.
题目详情
是否存在常数a、b、c使得等式1×2 2 +2×3 2 +3×4 2 +…+n(n+1) 2 =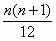 (an 2 +bn+c)对一切正整数n都成立?并证明你的结论.
(an 2 +bn+c)对一切正整数n都成立?并证明你的结论.
▼优质解答
答案和解析
答案:
解析:
∵n(n+1)2=n3+2n2+n, ∴Sn=1×22+2×32+3×42+…+n(n+1)2 =(13+2×12+1)+(23+2×22+2)+…+(n3+2×n2+n) =(13+23+…+n3)+2(12+22+…+n2)+(1+2+…+n). 由于下列等式对正整数n都成立, 13+23+…+n3=, 12+22+…+n2=, 1+2+…+n=. 由此可知Sn=(3n2+11n+10). 综上所述,当a=3,b=11,c=10时,题设的等式对一切正整数n都成立.
分 析:
数列求和在数列中占有重要的位置,有关存在性、探索性的问题是检验学生能力的关键所在.
解析:
∵n(n+1)2=n3+2n2+n, ∴Sn=1×22+2×32+3×42+…+n(n+1)2 =(13+2×12+1)+(23+2×22+2)+…+(n3+2×n2+n) =(13+23+…+n3)+2(12+22+…+n2)+(1+2+…+n). 由于下列等式对正整数n都成立, 13+23+…+n3=, 12+22+…+n2=, 1+2+…+n=. 由此可知Sn=(3n2+11n+10). 综上所述,当a=3,b=11,c=10时,题设的等式对一切正整数n都成立.
分 析:
数列求和在数列中占有重要的位置,有关存在性、探索性的问题是检验学生能力的关键所在.
看了 是否存在常数a、b、c使得等...的网友还看了以下:
定义一种对正整数n的F运算定义一种对正整数n的"F"运算1.当n为奇数时,结果为3n+5;2.当n 2020-04-06 …
定义一种对正整数n定义一种对正数n的“F”运算:一、当n为奇数时结果为3n+5;二、当n为偶数时, 2020-04-06 …
正整数n(n>1)的三次方分解为m个连续奇数之和,n是质数的时候只有一种吗?正整数n,n是质数的时 2020-04-10 …
定义一种对正整数n的“ F运算”:(1)当n为奇数是,记过为3n+5;(2)当n为偶数时,结果为n 2020-05-13 …
定义一种对正整数n的f运算定义一种对正整数n的"F"运算1.当n为奇数时,结果为3n+5;2.当n 2020-05-22 …
求教数学题一道如果n是一个大于6的整数,那下面哪一个一定能被3整除?A.N*(N+5)(N-6)B 2020-06-12 …
(1).y^2-13y+12(2)对于任意整数,n,n^2-n必是偶数(3)关于x的二次三项式x^ 2020-07-31 …
用数学归纳法证明:证明:对大于2的一切正整数n证明:对大于2的一切正整数n,下列不等式成立(1+2 2020-08-01 …
定义一种对正整数n的“F”运算:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为n2k(其中k 2020-12-07 …
写出判断整数n(n>2)是否为质数的算法.第一步:给定大于2的整数n;第二步:令i=2;第三步:用i 2020-12-09 …