早教吧作业答案频道 -->数学-->
如图①,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm.点P从点A开始沿AB以1cm/s的速度向点B运动,同时点Q从B点开始沿BC以2cm/s的速度向点C运动,当点Q到达点C时运动结束.设移动的时间为t(S).(1)
题目详情
如图①,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm.点P从点A开始沿AB以1cm/s的速度向点B运动,同时点Q从B点开始沿BC以2cm/s的速度向点C运动,当点Q到达点C时运动结束.设移动的时间为t(S).
(1)如果P、Q分别从A、B同时出发,若△PBQ的面积等于5cm2,求此时t的值;
(2)如图②,若点Q到达点C后继续沿CA运动,当点P到达点B时运动结束,求当△PBQ的面积等于5cm2时t的值.
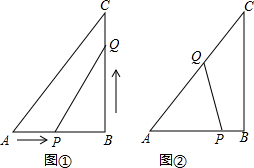
(1)如果P、Q分别从A、B同时出发,若△PBQ的面积等于5cm2,求此时t的值;
(2)如图②,若点Q到达点C后继续沿CA运动,当点P到达点B时运动结束,求当△PBQ的面积等于5cm2时t的值.

▼优质解答
答案和解析
(1)设经过t秒,△PBQ的面积等于5cm2则:
BP=6-t,BQ=2t,
所以S△PBQ=
×(6-t)×2t=5,
即t2-6t+5=0,
解得:t=1或t=5(不合题意,舍去),
即经过1秒时,△PBQ的面积等于5cm2.
(2)设出经t秒,点P移动到AC上,
则PB=6-t,AQ=(2t-8)cm,
如图②,
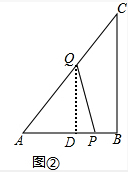
过Q作QD⊥AB,垂足为D,
∵△AQD∽△ABC,
∴
=
,
即QD=
,
×(6-t)×
=5
解得t=
,
当t=
时,2t>18,不合题意,舍去;
当t=
时,符合题意.
所以当△PBQ的面积等于5cm2时t=
.
BP=6-t,BQ=2t,
所以S△PBQ=
| 1 |
| 2 |
即t2-6t+5=0,
解得:t=1或t=5(不合题意,舍去),
即经过1秒时,△PBQ的面积等于5cm2.
(2)设出经t秒,点P移动到AC上,
则PB=6-t,AQ=(2t-8)cm,
如图②,

过Q作QD⊥AB,垂足为D,
∵△AQD∽△ABC,
∴
| QD |
| 8 |
| AQ |
| AC |
即QD=
| 8(18-2t) |
| 10 |
| 1 |
| 2 |
| 8(18-2t) |
| 10 |
解得t=
15±
| ||
| 2 |
当t=
15+
| ||
| 2 |
当t=
15-
| ||
| 2 |
所以当△PBQ的面积等于5cm2时t=
15-
| ||
| 2 |
看了 如图①,在Rt△ABC中,∠...的网友还看了以下:
曲线C以双曲线x22-y22=1的右焦点F为焦点,曲线C上的点到焦点F的距离与到直线x=-2的距离 2020-05-15 …
己知一个贮油罐横截面的外轮廓线是个椭圆,它的焦距为2.4m,外轮廓线上的点到两个焦点距离的和为3, 2020-05-15 …
抛物线外的点到抛物线上任意一点的最短距离如何求例如:y=x^2上的某点,到(16,1/2)的最短距 2020-05-20 …
三颗骰子得出的点数概率问题甩出三颗骰子...得到的总和为3,4,5,.16,17,18请问出现各个 2020-06-17 …
已知−12在数轴上所对应的点为A,数轴上点B、C在点A的两侧(点B在点A的右侧),且它们到点A的距 2020-06-19 …
椭圆的上的点到焦距的值为2a,椭圆的长轴的值也是2a,怎么区别?是不是说明椭圆的上的点到焦距的值就 2020-06-21 …
求曲线x3-xy+y3=1(x≥0,y≥0)上的点到坐标原点的最长距离和最短距离求曲线x3-xy+y 2020-10-31 …
在数轴上,表示一个数a的点到数b的点之间的距离,叫做a-b的绝对值,记作|a-b|.求在数轴上,表示 2020-11-20 …
将所带电荷量为q1=1.0*10-8C的点电荷,从无穷远处移到电场中的P点,需克服电场力做功2.0* 2020-12-15 …
以下关于距离的四种说法中正确的有?1.连接两点的线段长度叫做两点的距离;2.连接直线外一点和直线上的 2020-12-21 …