早教吧作业答案频道 -->数学-->
定义:如果一个点能与另外两个点构成直角三角形,则称这个点为另外两个点的勾股点.例如:在矩形OBCD中,点C是O、B两点的一个勾股点(如图1所示).问题(1):如图1,在矩形OBCD中,OD
题目详情
定义:如果一个点能与另外两个点构成直角三角形,则称这个点为另外两个点的勾股点.例如:在矩形OBCD中,点C是O、B两点的一个勾股点(如图1所示).
问题(1):如图1,在矩形OBCD中,OD=4,DC边上取一点E,DE=8.若点E是O、B两点的勾股点(点E不与点C重合),求OB的长;
问题(2):如图2,在矩形OBCD中,OD=4,OB=12,在OB边上取一点F,使OF=5,DC边上取一点E,使DE=8.点P为DC边上一动点,过点P作直线PQ∥OD交OB边于点Q.设DP=t(t>0).
①当点P在线段DE之间时,以EF为直径的圆与直线PQ相切,求t的值;
②若直PQ上恰好存在两个点是E、F两点的勾股点时,请直接写出求t的取值范围.
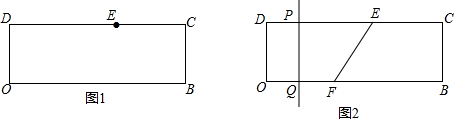
问题(1):如图1,在矩形OBCD中,OD=4,DC边上取一点E,DE=8.若点E是O、B两点的勾股点(点E不与点C重合),求OB的长;
问题(2):如图2,在矩形OBCD中,OD=4,OB=12,在OB边上取一点F,使OF=5,DC边上取一点E,使DE=8.点P为DC边上一动点,过点P作直线PQ∥OD交OB边于点Q.设DP=t(t>0).
①当点P在线段DE之间时,以EF为直径的圆与直线PQ相切,求t的值;
②若直PQ上恰好存在两个点是E、F两点的勾股点时,请直接写出求t的取值范围.

▼优质解答
答案和解析
(1)如图1所示,连接OE、BE.
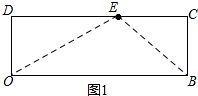
设OB=x,则EC=x-8.
在△DOE中,OE2=DE2+OD2=42+82=80,BE2=CE2+CB2=42+(x-8)2.
∵E为点O和点B的勾股定理点,
∴OB2=OE2+BE2,即42+(x-8)2+80=x2.
解得:x=10.
∴OB=10.
(2)①过点F作FG⊥DC,垂足为G,过点O作ON∥DE.
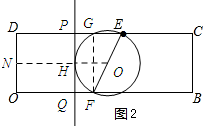
∵DE=8,OF=5,DO=4,
∴GE=3,FG=4,ON=6.5.
∴EF=
=5.
∴OH=2.5.
∴HN=NO-OH=6.5-2.5=4.
∴t=4.
②如图3所示:当直线PQ与圆O相离时.过点E作EG⊥EF交PQ于点G,过点F作HF⊥EF,垂足为H.
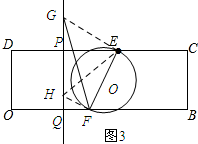
∵∠GEF=90°,
∴△GEF为直角三角形.
∴G是E、F的一个公共点.
同理点H也是E、F的一个公共点.
∴当直线PQ与圆O相离时,PQ上恰好存在两个点是E、F两点的勾股点.
∴当0<t<4时,PQ上恰好存在两个点是E、F两点的勾股点.
同理:当PQ在圆O的右侧,PQ上恰好存在两个点是E、F两点的勾股点.
∴9<t≤12.
如图4所示:当PF经过点F时,PQ上恰好存在两个点是E、F两点的勾股点.
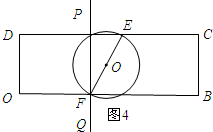
∵OF=5,
∴t=5.
如图5所示:当PF经过点E时,PQ上恰好存在两个点是E、F两点的勾股点.
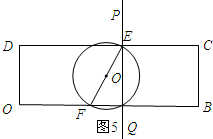
∵DE=8,
∴t=8.
综上所述当0<t<4或t=5或t=8或9<t≤12时,PQ上恰好存在两个点是E、F两点的勾股点.

设OB=x,则EC=x-8.
在△DOE中,OE2=DE2+OD2=42+82=80,BE2=CE2+CB2=42+(x-8)2.
∵E为点O和点B的勾股定理点,
∴OB2=OE2+BE2,即42+(x-8)2+80=x2.
解得:x=10.
∴OB=10.
(2)①过点F作FG⊥DC,垂足为G,过点O作ON∥DE.

∵DE=8,OF=5,DO=4,
∴GE=3,FG=4,ON=6.5.
∴EF=
| GE2+FG2 |
∴OH=2.5.
∴HN=NO-OH=6.5-2.5=4.
∴t=4.
②如图3所示:当直线PQ与圆O相离时.过点E作EG⊥EF交PQ于点G,过点F作HF⊥EF,垂足为H.

∵∠GEF=90°,
∴△GEF为直角三角形.
∴G是E、F的一个公共点.
同理点H也是E、F的一个公共点.
∴当直线PQ与圆O相离时,PQ上恰好存在两个点是E、F两点的勾股点.
∴当0<t<4时,PQ上恰好存在两个点是E、F两点的勾股点.
同理:当PQ在圆O的右侧,PQ上恰好存在两个点是E、F两点的勾股点.
∴9<t≤12.
如图4所示:当PF经过点F时,PQ上恰好存在两个点是E、F两点的勾股点.

∵OF=5,
∴t=5.
如图5所示:当PF经过点E时,PQ上恰好存在两个点是E、F两点的勾股点.

∵DE=8,
∴t=8.
综上所述当0<t<4或t=5或t=8或9<t≤12时,PQ上恰好存在两个点是E、F两点的勾股点.
看了 定义:如果一个点能与另外两个...的网友还看了以下:
小学数学问题,快点回答,要详细的过程1.用1根长绳来测量井的深度,如果把绳子3折来量,井外余4米, 2020-06-05 …
函数F(x)=根号下(4+2x-x²)-1,减1在根号外.如何证明这个函数的曲线图是一个圆的一部分 2020-06-07 …
如图,已知在△ABC中,∠1=∠2.(1)请你添加一个与直线AC有关的条件,由此可得出BE是△AB 2020-06-13 …
现有一些(乐高)的积木,其中4个头的一个如1-2-4-2-1是一种摆放方式,一共有多少种摆放方式? 2020-06-22 …
1.2.3.4.5.6.7.8.9.10十个数字分成三个不相同的数字一组,如1.2.3就不能有21 2020-07-19 …
1/3+1/3+6+1/3+6+9+.1/3+6+9+12+.+237+300注意例如1/3=三分 2020-07-19 …
铁路施工中,轨道工程平均每公里的造价为多少?对于铁路专用线中,轨道工程平均每公里的造价为多少?如细 2020-07-21 …
一至一百的π值详细一点如:1*3.14=3.142*3.14=2.68 2020-07-26 …
如图,已知圆心O的半径为4,弦BC长为4倍根号3,点A为弦BC所对优弧上任意一点.(BC两点除外) 2020-07-26 …
如图,P是△ABC的∠BAC的外角平分线上的一点.(1)求证:PB+PC>AB+AC(2)若P是△ 2020-08-03 …