如图所示，穿有M、N两个小球（均视为质点）的光滑绝缘圆环，固定在竖直面内，圆心为O、半径为R=0.3m．M、N用一根不可伸长的绝缘轻质细绳相连，质量分别为mM=0.01kg、mN=0.08kg；M带电量q=+7×1

Question

如图所示，穿有M、N两个小球（均视为质点）的光滑绝缘圆环，固定在竖直面内，圆心为O、半径为R=0.3m．M、N用一根不可伸长的绝缘轻质细绳相连，质量分别为m_M=0.01kg、m_N=0.08kg；M带电量q=+7×10^-4C，N不带电．该空间同时存在匀强电场和匀强磁场．电场方向竖直向上，电场强度E=1×10³V/m；磁场方向垂直于圆环平面向里，磁感应强度B=(√(3))/(7)×10² T．将两小球从图示位置（M与圆心O等高，N在圆心O的正下方）由静止释放，两小球开始沿逆时针向上转动．取重力加速度g=10m/s²，已知sin37°=0.6，cos37°=0.8．则在两球从图示位置逆时针向上转动的过程中，求：

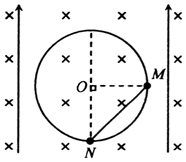
（1）通过计算判断，小球M能否到达圆环的最高点？
（2）小球M速度最大时，圆环对小球M的弹力．
（3）小球M电势能变化量的最大值．

Answer 1

{"title":"

1\uff09\u8bbeM\u3001N\u5728\u8f6c\u52a8\u8fc7\u7a0b\u4e2d\uff0c\u7ef3\u5bf9M\u3001N\u505a\u7684\u529f\u5206\u522b\u4e3aW_{T\u548cW\u2032T\uff0c\u5219\uff1a
WT+W\u2032T=0 
\u8bbeM\u5230\u8fbe\u5706\u73af\u6700\u9ad8\u70b9\u65f6\uff0cM\u3001N\u7684\u52a8\u80fd\u5206\u522b\u4e3aEKM\u3001EKN
\u5bf9M\uff0c\u6d1b\u4ed1\u5179\u529b\u4e0d\u505a\u529f\uff0c\u7531\u52a8\u80fd\u5b9a\u7406\u5f97\uff1aqER-mMgR+WT=EKM
\u5bf9N\uff0c\u7531\u52a8\u80fd\u5b9a\u7406\uff1aW\u2032T-mNgR=EKN
\u8054\u7acb\u89e3\u5f97\uff1aEKM+EKN=-0.06J
\u5373M\u5728\u5706\u73af\u6700\u9ad8\u70b9\u65f6\uff0c\u7cfb\u7edf\u52a8\u80fd\u4e3a\u8d1f\u503c\uff0c\u6545M\u4e0d\u80fd\u5230\u8fbe\u5706\u73af\u6700\u9ad8\u70b9\uff0e
\uff082\uff09\u8bbeN\u8f6c\u8fc7\u03b1\u89d2\u65f6\uff0cM\u3001N\u7684\u901f\u5ea6\u5927\u5c0f\u5206\u522b\u4e3avM\u3001vN\uff0c\u56e0M\u3001N\u505a\u5706\u5468\u8fd0\u52a8\u7684
\u534a\u5f84\u548c\u89d2\u901f\u5ea6\u5747\u76f8\u540c\uff0c\u6545\uff1avM=vN
\u5bf9M\uff0c\u6d1b\u4ed1\u5179\u529b\u4e0d\u505a\u529f\uff0c\u7531\u52a8\u80fd\u5b9a\u7406\uff1a}

\u5bf9N\uff0c\u7531\u80fd\u5b9a\u7406\uff1a

\u8054\u7acb\u89e3\u5f97\uff1a

\u7531\u4e0a\u5f0f\u53ef\u5f97\uff0c\u5f53\uff08\u5373\uff09\u65f6\uff0cM\u3001N\u7684\u901f\u5ea6\u8fbe\u5230\u6700\u5927\uff0e\u6700\u5927\u901f\u5ea6\u4e3a\uff1a

M\u901f\u5ea6\u6700\u5927\u65f6\uff0c\u8bbe\u7ef3\u5b50\u62c9\u529b\u4e3aF\uff0c\u5706\u73af\u5bf9\u5c0f\u7403M\u7684\u5f39\u529b\u4e3aFN\uff0c\u7531\u725b\u987f\u7b2c\u4e8c\u5b9a\u5f8b\u5f97\uff1a

\u89e3\u5f97\uff1aF_{N=-0.096N   \u8d1f\u53f7\u8868\u793a\u5f39\u529b\u65b9\u5411\u6cbf\u5706\u73af\u5f84\u5411\u5411\u5916\uff0e
\uff083\uff09M\u3001N\u4ece\u56fe\u793a\u4f4d\u7f6e\u9006\u65f6\u9488\u8f6c\u52a8\u8fc7\u7a0b\u4e2d\uff0c\u7531\u4e8eM\u4e0d\u80fd\u5230\u8fbe\u6700\u9ad8\u70b9\uff0c\u6240\u4ee5\uff0c\u5f53\u4e24\u7403
\u901f\u5ea6\u4e3a0\u65f6\uff0c\u7535\u573a\u529b\u505a\u529f\u6700\u591a\uff0c\u7535\u52bf\u80fd\u51cf\u5c11\u6700\u591a\uff0e}

\u7531

\u5f97\uff1a3sin\u03b1+4cos\u03b1-4=0
\u89e3\u5f97\uff1a\u6216sin\u03b1=0\uff08\u820d\u53bb\uff09
\u6545M\u7684\u7535\u52bf\u80fd\u51cf\u5c11\u91cf\u7684\u6700\u5927\u503c\u4e3a\uff1a

\u7b54\uff1a\uff081\uff09\u901a\u8fc7\u8ba1\u7b97\u5224\u65ad\uff0c\u5c0f\u7403M\u4e0d\u80fd\u5230\u8fbe\u5706\u73af\u7684\u6700\u9ad8\u70b9\uff0e
\uff082\uff09\u5c0f\u7403M\u901f\u5ea6\u6700\u5927\u65f6\uff0c\u5706\u73af\u5bf9\u5c0f\u7403M\u7684\u5f39\u529b\u4e3a0.096N\uff0c\u65b9\u5411\u6cbf\u5706\u73af\u5f84\u5411\u5411\u5916\uff0e
\uff083\uff09\u5c0f\u7403M\u7535\u52bf\u80fd\u53d8\u5316\u91cf\u7684\u6700\u5927\u503c\u662f0.2016J\uff0e

" "latex":"

1\uff09\u8bbeM\u3001N\u5728\u8f6c\u52a8\u8fc7\u7a0b\u4e2d\uff0c\u7ef3\u5bf9M\u3001N\u505a\u7684\u529f\u5206\u522b\u4e3aW_{T\u548cW\u2032T\uff0c\u5219\uff1a
WT+W\u2032T=0 
\u8bbeM\u5230\u8fbe\u5706\u73af\u6700\u9ad8\u70b9\u65f6\uff0cM\u3001N\u7684\u52a8\u80fd\u5206\u522b\u4e3aEKM\u3001EKN
\u5bf9M\uff0c\u6d1b\u4ed1\u5179\u529b\u4e0d\u505a\u529f\uff0c\u7531\u52a8\u80fd\u5b9a\u7406\u5f97\uff1aqER-mMgR+WT=EKM
\u5bf9N\uff0c\u7531\u52a8\u80fd\u5b9a\u7406\uff1aW\u2032T-mNgR=EKN
\u8054\u7acb\u89e3\u5f97\uff1aEKM+EKN=-0.06J
\u5373M\u5728\u5706\u73af\u6700\u9ad8\u70b9\u65f6\uff0c\u7cfb\u7edf\u52a8\u80fd\u4e3a\u8d1f\u503c\uff0c\u6545M\u4e0d\u80fd\u5230\u8fbe\u5706\u73af\u6700\u9ad8\u70b9\uff0e
\uff082\uff09\u8bbeN\u8f6c\u8fc7\u03b1\u89d2\u65f6\uff0cM\u3001N\u7684\u901f\u5ea6\u5927\u5c0f\u5206\u522b\u4e3avM\u3001vN\uff0c\u56e0M\u3001N\u505a\u5706\u5468\u8fd0\u52a8\u7684
\u534a\u5f84\u548c\u89d2\u901f\u5ea6\u5747\u76f8\u540c\uff0c\u6545\uff1avM=vN
\u5bf9M\uff0c\u6d1b\u4ed1\u5179\u529b\u4e0d\u505a\u529f\uff0c\u7531\u52a8\u80fd\u5b9a\u7406\uff1a$qERsin\\alpha -{m}_{M}gsin\\alpha +{W}_{T2}=\\dfrac {1} {2}{m}_{M}{v}^{2}_{M}$}

\u5bf9N\uff0c\u7531\u80fd\u5b9a\u7406\uff1a

${W}_{T2}-{m}_{N}gR\uff081-cos\\alpha \uff09=\\dfrac {1} {2}{m}_{M}{v}^{2}_{M}$

\u8054\u7acb\u89e3\u5f97\uff1a${v}^{2}_{M}=\\dfrac {4} {3}\\times \uff083sin\\alpha +4cos\\alpha -4\uff09$

\u7531\u4e0a\u5f0f\u53ef\u5f97\uff0c\u5f53$tan\\alpha =\\dfrac {3} {4}$\uff08\u5373$\\alpha =37\u00b0$\uff09\u65f6\uff0cM\u3001N\u7684\u901f\u5ea6\u8fbe\u5230\u6700\u5927\uff0e\u6700\u5927\u901f\u5ea6\u4e3a\uff1a${v}_{max}=\\dfrac {23} {2}m\/s$

M\u901f\u5ea6\u6700\u5927\u65f6\uff0c\u8bbe\u7ef3\u5b50\u62c9\u529b\u4e3aF\uff0c\u5706\u73af\u5bf9\u5c0f\u7403M\u7684\u5f39\u529b\u4e3aFN\uff0c\u7531\u725b\u987f\u7b2c\u4e8c\u5b9a\u5f8b\u5f97\uff1a
$Fcos45\u00b0=\uff08qE-{m}_{M}g\uff09cos7\u00b0$

$q{v}_{max}B+Fsin45\u00b0-\uff08qE-{m}_{M}g\uff09sin37\u00b0+{F}_{N}={m}_{M}\\dfrac {{v}^{2}_{M}} {R}$

\u89e3\u5f97\uff1aF_{N=-0.096N   \u8d1f\u53f7\u8868\u793a\u5f39\u529b\u65b9\u5411\u6cbf\u5706\u73af\u5f84\u5411\u5411\u5916\uff0e
\uff083\uff09M\u3001N\u4ece\u56fe\u793a\u4f4d\u7f6e\u9006\u65f6\u9488\u8f6c\u52a8\u8fc7\u7a0b\u4e2d\uff0c\u7531\u4e8eM\u4e0d\u80fd\u5230\u8fbe\u6700\u9ad8\u70b9\uff0c\u6240\u4ee5\uff0c\u5f53\u4e24\u7403
\u901f\u5ea6\u4e3a0\u65f6\uff0c\u7535\u573a\u529b\u505a\u529f\u6700\u591a\uff0c\u7535\u52bf\u80fd\u51cf\u5c11\u6700\u591a\uff0e}

\u7531${v}^{2}_{M}=\\dfrac {4} {3}\uff083sin\\alpha +4co\\alpha -4\uff09$

\u5f97\uff1a3sin\u03b1+4cos\u03b1-4=0
\u89e3\u5f97\uff1a$sin\\alpha =\\dfrac {24} {25}$\u6216sin\u03b1=0\uff08\u820d\u53bb\uff09
\u6545M\u7684\u7535\u52bf\u80fd\u51cf\u5c11\u91cf\u7684\u6700\u5927\u503c\u4e3a\uff1a
$\\left | {\\triangle E} \\right |=qERsin\\alpha =\\dfrac {126} {625}J=0.2016J$

\u7b54\uff1a\uff081\uff09\u901a\u8fc7\u8ba1\u7b97\u5224\u65ad\uff0c\u5c0f\u7403M\u4e0d\u80fd\u5230\u8fbe\u5706\u73af\u7684\u6700\u9ad8\u70b9\uff0e
\uff082\uff09\u5c0f\u7403M\u901f\u5ea6\u6700\u5927\u65f6\uff0c\u5706\u73af\u5bf9\u5c0f\u7403M\u7684\u5f39\u529b\u4e3a0.096N\uff0c\u65b9\u5411\u6cbf\u5706\u73af\u5f84\u5411\u5411\u5916\uff0e
\uff083\uff09\u5c0f\u7403M\u7535\u52bf\u80fd\u53d8\u5316\u91cf\u7684\u6700\u5927\u503c\u662f0.2016J\uff0e

"}