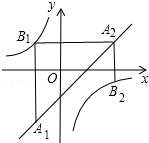
如图，已知点A1，A2，…，An均在直线y=x-1上，点B1，B2，…，Bn均在双曲线y=-1x上，并且满足：A1B1⊥x轴，B1A2⊥y轴，A2B2⊥x轴，B2A3⊥y轴，…，AnBn⊥x轴，BnAn+1⊥y轴，…，记

Question

如图，已知点A₁，A₂，…，A_n均在直线y=x-1上，点B₁，B₂，…，B_n均在双曲线y=- (1)/(x) 上，并且满足：A₁B₁⊥x轴，B₁A₂⊥y轴，A₂B₂⊥x轴，B₂A₃⊥y轴，…，A_nB_n⊥x轴，B_nA_n+1⊥y轴，…，记点A_n的横坐标为a_n（n为正整数）．若a₁=-1，则a₂₀₁₆=___．

Answer 1

∵a₁=-1，
∴B₁的坐标是（-1，1），
∴A₂的坐标是（2，1），
即a₂=2，
∵a₂=2，
∴B₂的坐标是（2，-(1)/(2)），
∴A₃的坐标是（(1)/(2)，-(1)/(2)），
即a₃=(1)/(2)，
∵a₃=(1)/(2)，
∴B₃的坐标是（(1)/(2)，-2），
∴A₄的坐标是（-1，-2），
即a₄=-1，
∵a₄=-1，
∴B₄的坐标是（-1，1），
∴A₅的坐标是（2，1），
即a₅=2，
…，
∴a₁，a₂，a₃，a₄，a₅，…，每3个数一个循环，分别是-1、2、(1)/(2)，
∵2016÷3=672，
∴a₂₀₁₆是第672个循环的第3个数，
∴a₂₀₁₆=(1)/(2)．
故答案为：(1)/(2)．