早教吧作业答案频道 -->数学-->
如图,在△ABC中,AB=c,AC=b.AD是△ABC的角平分线,DE⊥A于E,DF⊥AC于F,EF与AD相交于O,已知△ADC的面积为1.(1)证明:DE=DF;(2)试探究线段EF和AD是否垂直?并说明理由;(3)若△BDE的
题目详情
如图,在△ABC中,AB=c,AC=b.AD是△ABC的角平分线,DE⊥A于E,DF⊥AC于F,EF与AD相交于O,已知△ADC的面积为1.
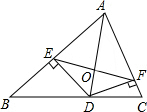
(1)证明:DE=DF;
(2)试探究线段EF和AD是否垂直?并说明理由;
(3)若△BDE的面积是△CDF的面积2倍.试求四边形AEDF的面积.

(1)证明:DE=DF;
(2)试探究线段EF和AD是否垂直?并说明理由;
(3)若△BDE的面积是△CDF的面积2倍.试求四边形AEDF的面积.
▼优质解答
答案和解析
(1)证明:
∵AD是△ABC的角平分线,DE⊥A于E,DF⊥AC于F,
∴DE=DF(角平分线的性质);
(2)垂直.理由如下:
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中
,
∴Rt△AED≌Rt△AFD(AAS),
∴AE=AF,
∴点A在线段EF的垂直平分线上,
同理点D也在线段EF的垂直平分线上,
∴AD⊥EF;
(3)设S△CDF=x,则S△BDE=2x,
∵S△ACD=1,且△AED≌△AFD,
∴S△AED=S△AFD=1-x,
∴S△ABD=S△BDE+S△AED=2x+1-x=x+1,
又S△ABD=
AB•DE,S△ACD=
AC•DF,且AB=c,AC=b,
∴
×c•DE=x+1,
×b•DF=1,
∴DE=
,DF=
,
又由(1)可知DE=DF,
∴
=
,解得x=
-1,
∵△AED≌△AFD,
∴S△AED=S△AFD=S△ACD-S△CDF=1-x,
∴S四边形AEDF=2S△AED=2(1-x)=2[1-(
-1)]=4-
,
即四边形AEDF的面积为4-
.
(1)证明:
∵AD是△ABC的角平分线,DE⊥A于E,DF⊥AC于F,
∴DE=DF(角平分线的性质);
(2)垂直.理由如下:
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中
|
∴Rt△AED≌Rt△AFD(AAS),
∴AE=AF,
∴点A在线段EF的垂直平分线上,
同理点D也在线段EF的垂直平分线上,
∴AD⊥EF;
(3)设S△CDF=x,则S△BDE=2x,
∵S△ACD=1,且△AED≌△AFD,
∴S△AED=S△AFD=1-x,
∴S△ABD=S△BDE+S△AED=2x+1-x=x+1,
又S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴DE=
| 2x+2 |
| c |
| 2 |
| b |
又由(1)可知DE=DF,
∴
| 2x+2 |
| c |
| 2 |
| b |
| c |
| b |
∵△AED≌△AFD,
∴S△AED=S△AFD=S△ACD-S△CDF=1-x,
∴S四边形AEDF=2S△AED=2(1-x)=2[1-(
| c |
| b |
| 2c |
| b |
即四边形AEDF的面积为4-
| 2c |
| b |
看了 如图,在△ABC中,AB=c...的网友还看了以下:
关于2阶矩阵的伴随矩阵2阶矩阵为abcd为什么它的伴随矩阵不是d-c-ba按照定义不就应该是这样的 2020-04-13 …
一道英语选择题:有关数词形容名词Toplantthetree,wemustdig.A.athree 2020-04-27 …
已知直线m经过两点(1,6)(-3,-2),他和x轴、y轴的交点是B,A,直线n过点(2,-2)且 2020-06-21 …
怎样求下行数列的代数余子式请教高手!二阶行列式abcd很简单但是我我不会求他的代数余子式,请高手给 2020-08-03 …
ABCD四个同学有一个在体育比赛中获奖,老师问他们是谁?A说不是我,B说是D,C说是B,D说不是我 2020-08-03 …
某班进行了一次数学测试,A,B,C,D有一人未得满分.A说是B,B说是D,C说不是我,D说B说错了. 2020-11-07 …
对于“树立法治观念”的理解全面正确的是()A.敢于主持正义,制裁违法行为B.学习法律知识,善于明辨是 2020-12-21 …
⒈A、B、C、D4人中有一人体育未达标,当有人问他们是谁体育未达标时,A说:“是B”,B说:“是D” 2020-12-24 …
⒈A、B、C、D4人中有一人体育未达标,当有人问他们是谁体育未达标时,A说:“是B”,B说:“是D” 2020-12-24 …
一条数学图形请先画图:一个梯形,上面字母是A,B下面是D,C按左到右顺序E为AD中点,注意:AD是腰 2020-12-25 …