对于某些三角形或是四边形，我们可以直接用面积公式或是用割补法等来求它们的面积，下面我们研究一种求面积的新方法：如图1、2所示，分别过三角形或是四边形的顶点A、C作水平线的铅

Question

对于某些三角形或是四边形，我们可以直接用面积公式或是用割补法等来求它们的面积，下面我们研究一种求面积的新方法：
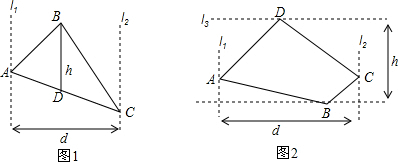
如图1、2所示，分别过三角形或是四边形的顶点A、C作水平线的铅垂线l₁、l₂，l₁、l₂之间的距离d叫做水平宽；如图1所示，过点B作水平线的铅垂线交AC于点D，称线段BD的长叫做这个三角形的铅垂高；如图2所示，分别过四边形的顶点B、D作水平线l₃、l₄，l₃、l₄之间的距离h叫做四边形的铅垂高．

【结论提炼】：容易证明：“三角形的面积等于水平宽与铅垂高乘积的一半”，即“S= (1)/(2)dh”．
【尝试应用】：
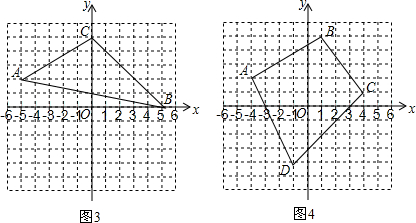
已知：如图3，点A（-5，2）、B（5，0）、C（0，5），则△ABC的水平宽为___，铅垂高为___，所以△ABC的面积为___．
【再探新知】：

三角形的面积可以用“水平宽与铅垂高乘积的一半”来求，那四边形的面积是不是也可以这样求呢？带着这个问题，小明进行了如下探索尝试：
（1）他首先在图4所示的平面直角坐标系中，取了A（-4，2）、B（1，5）、C（4，1）、D（-1，-4）四个点，得到了四边形ABCD．
小明运用“水平宽与铅垂高乘积的一半”进行计算的结果是___；他又用其它的方法进行了计算，结果是___，由此他发现：用“S= (1)/(2)dh”这一方法对图4中的四边形求面积___（填“适合”或“不适合”）．

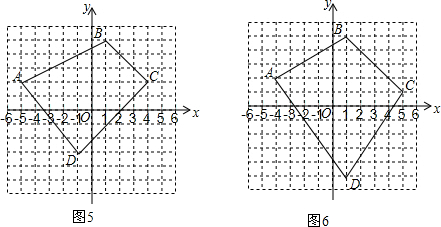
（2）小明并没有放弃尝试，他又在图5所示的平面直角坐标系中，取了A（-5，2）、B（1，5）、C（4，2）、D（-1，-3）四个点，得到了四边形ABCD．小明运用“水平宽与铅垂高乘积的一半”进行计算的结果是___，由此他发现：用“S= (1)/(2)dh”这一方法对图5中的四边形求面积___（填“适合”或“不适合”）．
（3）小明很奇怪，就继续进行了进一步尝试，他在图6所示的平面直角坐标系中，取了A（-4，2）、B（1，5）、C（5，1）、D（1，-5）四个点，得到了四边形ABCD．通过计算他发现：用“S= (1)/(2)dh”这一方法对图6中的四边形求面积___（填“适合”或“不适合”）．
通过以上尝试，小明恍然大悟得出结论：当四边形满足___条件时，四边形可以用“S= (1)/(2)dh”来求面积．
【学以致用】：
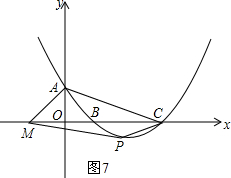
如图7，在平面直角坐标系中，点M坐标为（-2，0），抛物线的解析式为：y= (1)/(4)x²-2x+3，抛物线图象与y轴交于点A，与x轴交于B、C两点，点P为抛物线上一点，且位于B、C之间，请直接运用以上结论，写出当点P坐标为多少时，四边形AMPC面积最大．（直接写出P点坐标即可）

Answer 1

（1）小明运用“水平宽与铅垂高乘积的一半”进行计算的结果是36；他又用其它的方法进行了计算，结果是37，由此他发现：用“S=(1)/(2)dh”这一方法对图4中的四边形求面积不适合；
（2）小明运用“水平宽与铅垂高乘积的一半”进行计算的结果是36，由此他发现：用“S=(1)/(2)dh”这一方法对图5中的四边形求面积适合；
（3）通过计算他发现：用“S=(1)/(2)dh”这一方法对图6中的四边形求面积适合；
结论：当四边形满足一条对角线等于水平宽或铅垂高时，四边形可以用“S=(1)/(2)dh”来求面积．
y=(1)/(4)x²-2x+3的图象与y轴交于点A（0，3），
(1)/(4)x²-2x+3=0，解得，x₁=，x₂=6
与x轴交点B（2，0）、C（6，0），
当P点为抛物线的顶点时，四边形AMPC面积最大，
y=(1)/(4)x²-2x+3=(1)/(4)（x-4）²-1，∴顶点的坐标为（4，-1），
四边形AMPC的水平宽为8，铅垂高为4，
∴四边形AMPC面积为：(1)/(2)×8×4=16．