早教吧作业答案频道 -->数学-->
在直角△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC和∠BCA的平分线,AD,CE相交于点F.(1)求∠EFD的度数;(2)判断FE与FD之间的数量关系,并证明你的结论.
题目详情
在直角△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC和∠BCA的平分线,AD,CE相交于点F.
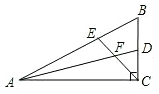
(1)求∠EFD的度数;
(2)判断FE与FD之间的数量关系,并证明你的结论.

(1)求∠EFD的度数;
(2)判断FE与FD之间的数量关系,并证明你的结论.
▼优质解答
答案和解析
(1)∵△ABC中,∠ACB=90°,∠B=60°
∴∠BAC=30°,
∵AD、CE分别是∠BAC、∠BCA的平分线
∴∠FAC=
∠BAC=15°,∠FCA=
∠ACB=45°
∴∠AFC=180°-∠FAC-∠FCA=120°,
∴∠EFD=∠AFC=120°;
(2)FE与FD之间的数量关系为FE=FD;
证明:在AC上截取AG=AE,连接FG,
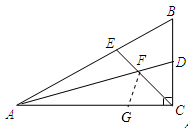
∵AD是∠BAC的平分线,∴∠1=∠2
又∵AF为公共边
在△EAF和△GAF中
∵
,
∴△AEF≌△AGF
∴FE=FG,∠AFE=∠AFG=60°,
∴∠CFG=60°,
又∵FC为公共边,∠DCF=∠FCG=45°
在△FDC和△FGC中
∵
,
∴△CFG≌△CFD,
∴FG=FD
∴FE=FD.
∴∠BAC=30°,
∵AD、CE分别是∠BAC、∠BCA的平分线
∴∠FAC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AFC=180°-∠FAC-∠FCA=120°,
∴∠EFD=∠AFC=120°;
(2)FE与FD之间的数量关系为FE=FD;
证明:在AC上截取AG=AE,连接FG,

∵AD是∠BAC的平分线,∴∠1=∠2
又∵AF为公共边
在△EAF和△GAF中
∵
|
∴△AEF≌△AGF
∴FE=FG,∠AFE=∠AFG=60°,
∴∠CFG=60°,
又∵FC为公共边,∠DCF=∠FCG=45°
在△FDC和△FGC中
∵
|
∴△CFG≌△CFD,
∴FG=FD
∴FE=FD.
看了 在直角△ABC中,∠ACB=...的网友还看了以下:
按照生物体结构层次的从小到大排列,正确的图形排序是()A.A→B→C→D→EB.C→E→A→D→B 2020-05-02 …
关于E=Fq和E=KQr2两个公式,下列说法中正确的是()A.E=Fq中的场强E是电荷q产生的B. 2020-05-13 …
设栈S的初始状态为空,元素a,b,c,d,e,f依次入栈S,出栈的序列为b,d,f,e,c,a…… 2020-05-17 …
∫0−π(cosx+ex)dx=()A.1-e-πB.1+e-πC.-e-πD.πe-π-1 2020-05-17 …
如图是膝跳反射的示意图,请根据你所知道的回答第21~23小题:该反射的神经传导通路的顺序是()A. 2020-06-28 …
如图是膝跳反射的示意图,请根据你所知道的回答第37~40小题:该反射的神经传导通路的顺序是()A. 2020-06-28 …
设A为n阶非零矩阵,E为n阶单位矩阵.若A3=0,则()A.E-A不可逆,E+A不可逆B.E-A不 2020-07-22 …
已知向量a≠e,|e|=1,对任意t∈R,恒有|a-te|≥|a-e|,则[]A.a⊥eB.a⊥(a 2020-11-02 …
如图,点A、B、C、D、E、F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是()A. 2020-11-06 …
设投掷1颗骰子的点数为ξ,则()A.Eξ=3.5,Dξ=3.52B.Eξ=3.5,Dξ=C.Eξ=3 2020-12-30 …