已知AB是异面直线a,b的公垂线,a平面α,b平面β,且α∥β,求证:AB即是平面α与平面β的公垂线.
已知AB是异面直线a,b的公垂线,a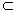 平面α,b
平面α,b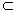 平面β,且α∥β,求证:AB即是平面α与平面β的公垂线.
平面β,且α∥β,求证:AB即是平面α与平面β的公垂线.
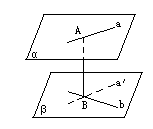
解析:
|
| 证明 经过相交直线a和AB的平面与平面β相交于经过B的一条直线 说明 利用此题结论,可将求两条异面直线的距离转化为求两个平行平面的距离. |
关于变异的说法,不正确的是()A.凡是外界环境引起的变异都是不可遗传的变异B.由遗传物质变化引起的 2020-05-14 …
已知P是平行四边形ABCD所在平面外一点,M,N分别为AB PC中点,若MN=BC=4已知P是平行 2020-05-15 …
已知ABCD是平行四边形,且AB=1,BC=2,角ABC=60°,PA⊥平面ABCD,PA=根号3 2020-05-16 …
鸟飞鹅跳,月上中梢,目上朱砂,已异非巳,勺旁傍白,万事开头,工戈不全,雨下挚友,称断人和,一句一. 2020-06-15 …
各抒己见赞叹不已异口同声表示(的词语)各表各抒己见赞叹不已异口同声表示(的词语)各表示什么 2020-06-21 …
您好!1.我也要做差异基因表达这方面的实验,但是我们不是看某个已知基因的表达差异,而是想看看有哪些 2020-06-26 …
已知p是rt△abc的斜边ab上异于a、b的一点,过点p作直线截△abc,使截得的三角形与△已知P 2020-07-07 …
某海岛经常有暴风雨,科学家发现该岛上的某种昆虫有两种类型:一种翅特别发达,另一种则已退化,由此说明 2020-07-12 …
已知AB是异面直线l1、l2的公垂线段,且AB=3,异面直线l1、l2成30°角,在直线l1上取A 2020-08-01 …
数学.1.如图,已知α∈β=a,b含于β,a∩b=A,且c含于α,c‖a,求证b与c为异面直线2. 2020-08-02 …
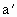 ,则
,则