早教吧作业答案频道 -->数学-->
平面外ABC的一点P,AP、AB、AC两两互相垂直,过AC的中点D做ED⊥面ABC,且ED=1,PA=2,AC=2,连接BP,BE,多面体B-PADE的体积是33;(1)画出面PBE与面ABC的交线,说明理由;(2)求BE与面PADE所成的
题目详情
平面外ABC的一点P,AP、AB、AC两两互相垂直,过AC的中点D做ED⊥面ABC,且ED=1,PA=2,AC=2,连接BP,BE,多面体B-PADE的体积是
;
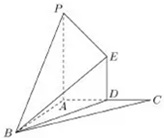
(1)画出面PBE与面ABC的交线,说明理由;
(2)求BE与面PADE所成的线面角的大小.
| ||
| 3 |

(1)画出面PBE与面ABC的交线,说明理由;
(2)求BE与面PADE所成的线面角的大小.
▼优质解答
答案和解析
(1)延长PE交AC于F,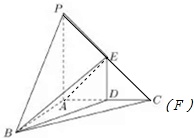
∵AP、AB、AC两两互相垂直,∴PA⊥平面ABC,
∵DE⊥平面ABC,
∴DE∥PA,
∴
=
=
,
∴F与C重合.
∵C∈PE,C∈AC,PE⊂平面PBE,AC⊂平面ABC,
∴C是平面PBE和平面ABC的公共点,
又B是平面PBE和平面ABC的公共点,
∴BC是面PBE与面ABC的交线.
(2)连接AE,
∵AP、AB、AC两两互相垂直,
∴AB⊥平面PAC,∴∠BEA为BE与平面PAD所成的角,
∴VB-PADE=
S梯形ADEP•AB=
×
×(1+2)×1×AB=
,
∴AB=
.
又∵AE=
=
,
∴tan∠BEA=
=
.
∴BE与面PADE所成的线面角为arctan
.

∵AP、AB、AC两两互相垂直,∴PA⊥平面ABC,
∵DE⊥平面ABC,
∴DE∥PA,
∴
| DF |
| AF |
| DE |
| PA |
| 1 |
| 2 |
∴F与C重合.
∵C∈PE,C∈AC,PE⊂平面PBE,AC⊂平面ABC,
∴C是平面PBE和平面ABC的公共点,
又B是平面PBE和平面ABC的公共点,
∴BC是面PBE与面ABC的交线.
(2)连接AE,
∵AP、AB、AC两两互相垂直,
∴AB⊥平面PAC,∴∠BEA为BE与平面PAD所成的角,
∴VB-PADE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 3 |
∴AB=
2
| ||
| 3 |
又∵AE=
| AD2+DE2 |
| 2 |
∴tan∠BEA=
| AB |
| AE |
| ||
| 3 |
∴BE与面PADE所成的线面角为arctan
| ||
| 3 |
看了 平面外ABC的一点P,AP、...的网友还看了以下:
长方体,面对你.且你看的到的所有面的面积公式知道给100分 2020-05-13 …
1.在写一个句子前面用不用空两格呢?2.外侧面是指他的露出的所有面还是侧面? 2020-05-15 …
关于正方体的应用题把一个表面积是170平方厘米的正方体木块,锯成几个体积相等的且没有剩余体积的最大 2020-05-20 …
地面防水层工程量,按主墙间净面积以m2计,应扣除地面的( )所占面积。 A.0.3m2孔洞B. 2020-06-07 …
“历史材料给我们今天所形成的印记,不能完全反照当时社会的所有面貌.”这句话是谁说? 2020-06-08 …
下列几何体的所有面都不是平面图形的是()A正方体B圆锥C圆柱D球 2020-06-14 …
右图是一个表面涂上蓝色的棱长4厘的正方体木,如果把它沿著虚线切成8个正方体,这些中没有被涂上蓝色的 2020-06-19 …
求教城管执法的依据,以及执法的范围咱在一小地方有一门面,卷闸门于门面滴水线距离还有1.5米,城管说 2020-06-23 …
有四个命题:①各侧面是全等的等腰三角形的四棱锥是正四棱锥;②底面是正多边形的棱锥是正棱锥;③棱锥的 2020-06-27 …
已知一个三棱柱,其底面是正三角形,且侧棱与底面垂直,一个体积为4π3的球体与棱柱的所有面均相切,那 2020-06-27 …