早教吧作业答案频道 -->数学-->
某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:(1)操作发现:在等腰△ABC中,AB=AC,分别以AB、AC为斜边,向△ABC的外侧作等腰直角三角形,如图1所示,其中DF⊥
题目详情
某数学活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:
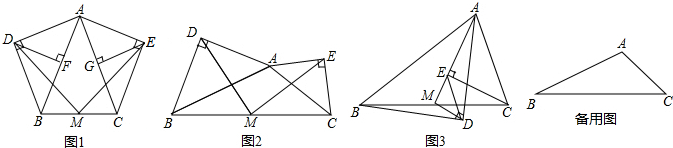
(1)操作发现:在等腰△ABC中,AB=AC,分别以AB、AC为斜边,向△ABC的外侧作等腰直角三角形,如图1所示,其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连结MD和ME,则下列结论正确的是___(填序号即可).
AF=AG=
AB;②MD=ME;③整个图形是轴对称图形;④MD⊥ME.
(2)数学思考:在任意△ABC中,分别以AB、AC为斜边,向△ABC的外侧作等腰直角三角形,如图2所示,M是BC的中点,连结MD和ME,则MD与ME有怎样的数量关系?请给出证明过程;
(3)类比探究:在任意△ABC中,仍分别以AB、AC为斜边,向△ABC的内侧作等腰直角三角形,如图3所示,M是BC的中点,连结MD和ME,试判断△MDE的形状.
答:___.
AB;②MD=ME;③整个图形是轴对称图形;④MD⊥ME.
(2)数学思考:在任意△ABC中,分别以AB、AC为斜边,向△ABC的外侧作等腰直角三角形,如图2所示,M是BC的中点,连结MD和ME,则MD与ME有怎样的数量关系?请给出证明过程;
(3)类比探究:在任意△ABC中,仍分别以AB、AC为斜边,向△ABC的内侧作等腰直角三角形,如图3所示,M是BC的中点,连结MD和ME,试判断△MDE的形状.
答:___.

1 2 1 1 2 2

(1)操作发现:在等腰△ABC中,AB=AC,分别以AB、AC为斜边,向△ABC的外侧作等腰直角三角形,如图1所示,其中DF⊥AB于点F,EG⊥AC于点G,M是BC的中点,连结MD和ME,则下列结论正确的是___(填序号即可).
AF=AG=
| 1 |
| 2 |
(2)数学思考:在任意△ABC中,分别以AB、AC为斜边,向△ABC的外侧作等腰直角三角形,如图2所示,M是BC的中点,连结MD和ME,则MD与ME有怎样的数量关系?请给出证明过程;
(3)类比探究:在任意△ABC中,仍分别以AB、AC为斜边,向△ABC的内侧作等腰直角三角形,如图3所示,M是BC的中点,连结MD和ME,试判断△MDE的形状.
答:___.

| 1 |
| 2 |
(2)数学思考:在任意△ABC中,分别以AB、AC为斜边,向△ABC的外侧作等腰直角三角形,如图2所示,M是BC的中点,连结MD和ME,则MD与ME有怎样的数量关系?请给出证明过程;
(3)类比探究:在任意△ABC中,仍分别以AB、AC为斜边,向△ABC的内侧作等腰直角三角形,如图3所示,M是BC的中点,连结MD和ME,试判断△MDE的形状.
答:___.

| 1 |
| 2 |

▼优质解答
答案和解析
(1)通过操作和图形的轴对称性可以发现:①②③是正确的;
∵AB=AC,BM=CM,
∴AM⊥BC,
∴∠AMB=∠AMC=90°,
∵∠ADB=90°,
∴四边形ADBM四点共圆,
∴∠AMD=∠ABD=45°.
∵AM是对称轴,
∴∠AME=∠AMD=45°,
∴∠DME=90°,
∴MD⊥ME,故④正确,
故答案为:①②③④.
(2)MD=ME,
理由:如图1,取AB、AC的中点F、G,连接DF,MF,EG,MG,
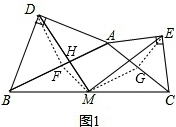
∴AF=
AB,AG=
AC.
∵△ABD和△AEC是等腰直角三角形,
∴DF⊥AB,DF=
AB,EG⊥AC,EG=
AC,
∴∠AFD=∠AGE=90°,DF=AF,GE=AG.
∵M是BC的中点,
∴MF∥AC,MG∥AB,
∴四边形AFMG是平行四边形,
∴AG=MF,MG=AF,∠AFM=∠AGM.
∴MF=GE,DF=MG,∠AFM+∠AFD=∠AGM+∠AGE,
∴∠DFM=∠MGE.
在△DFM和△MGE中,
,
∴△DFM≌△MGE(SAS),
∴DM=ME;
(3)如图2,取BC、AB和AC的中点M、F、G,连接MF、DF、MG、EG.
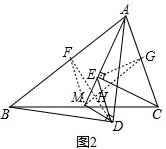
∴MF∥AC,MF=
AC,MG∥AB,MG=
AB,
∴四边形MFAG是平行四边形,
∴MG=AF,MF=AG,∠AFM=∠AGM,
∵△ADB和△AEC是等腰直角三角形,
∴DF=AF,GE=AG,∠AFD=∠BFD=∠AGE=90°,
∴MF=EG,DF=MG,∠AFM-∠AFD=∠AGM-∠AGE,
即∠DFM=∠MGE.
在△DFM和△MGE中,
,
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
1 2 1 1 12 2 2AB,AG=
AC.
∵△ABD和△AEC是等腰直角三角形,
∴DF⊥AB,DF=
AB,EG⊥AC,EG=
AC,
∴∠AFD=∠AGE=90°,DF=AF,GE=AG.
∵M是BC的中点,
∴MF∥AC,MG∥AB,
∴四边形AFMG是平行四边形,
∴AG=MF,MG=AF,∠AFM=∠AGM.
∴MF=GE,DF=MG,∠AFM+∠AFD=∠AGM+∠AGE,
∴∠DFM=∠MGE.
在△DFM和△MGE中,
,
∴△DFM≌△MGE(SAS),
∴DM=ME;
(3)如图2,取BC、AB和AC的中点M、F、G,连接MF、DF、MG、EG.

∴MF∥AC,MF=
AC,MG∥AB,MG=
AB,
∴四边形MFAG是平行四边形,
∴MG=AF,MF=AG,∠AFM=∠AGM,
∵△ADB和△AEC是等腰直角三角形,
∴DF=AF,GE=AG,∠AFD=∠BFD=∠AGE=90°,
∴MF=EG,DF=MG,∠AFM-∠AFD=∠AGM-∠AGE,
即∠DFM=∠MGE.
在△DFM和△MGE中,
,
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
1 2 1 1 12 2 2AC.
∵△ABD和△AEC是等腰直角三角形,
∴DF⊥AB,DF=
AB,EG⊥AC,EG=
AC,
∴∠AFD=∠AGE=90°,DF=AF,GE=AG.
∵M是BC的中点,
∴MF∥AC,MG∥AB,
∴四边形AFMG是平行四边形,
∴AG=MF,MG=AF,∠AFM=∠AGM.
∴MF=GE,DF=MG,∠AFM+∠AFD=∠AGM+∠AGE,
∴∠DFM=∠MGE.
在△DFM和△MGE中,
,
∴△DFM≌△MGE(SAS),
∴DM=ME;
(3)如图2,取BC、AB和AC的中点M、F、G,连接MF、DF、MG、EG.

∴MF∥AC,MF=
AC,MG∥AB,MG=
AB,
∴四边形MFAG是平行四边形,
∴MG=AF,MF=AG,∠AFM=∠AGM,
∵△ADB和△AEC是等腰直角三角形,
∴DF=AF,GE=AG,∠AFD=∠BFD=∠AGE=90°,
∴MF=EG,DF=MG,∠AFM-∠AFD=∠AGM-∠AGE,
即∠DFM=∠MGE.
在△DFM和△MGE中,
,
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
1 2 1 1 12 2 2AB,EG⊥AC,EG=
AC,
∴∠AFD=∠AGE=90°,DF=AF,GE=AG.
∵M是BC的中点,
∴MF∥AC,MG∥AB,
∴四边形AFMG是平行四边形,
∴AG=MF,MG=AF,∠AFM=∠AGM.
∴MF=GE,DF=MG,∠AFM+∠AFD=∠AGM+∠AGE,
∴∠DFM=∠MGE.
在△DFM和△MGE中,
,
∴△DFM≌△MGE(SAS),
∴DM=ME;
(3)如图2,取BC、AB和AC的中点M、F、G,连接MF、DF、MG、EG.

∴MF∥AC,MF=
AC,MG∥AB,MG=
AB,
∴四边形MFAG是平行四边形,
∴MG=AF,MF=AG,∠AFM=∠AGM,
∵△ADB和△AEC是等腰直角三角形,
∴DF=AF,GE=AG,∠AFD=∠BFD=∠AGE=90°,
∴MF=EG,DF=MG,∠AFM-∠AFD=∠AGM-∠AGE,
即∠DFM=∠MGE.
在△DFM和△MGE中,
,
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
1 2 1 1 12 2 2AC,
∴∠AFD=∠AGE=90°,DF=AF,GE=AG.
∵M是BC的中点,
∴MF∥AC,MG∥AB,
∴四边形AFMG是平行四边形,
∴AG=MF,MG=AF,∠AFM=∠AGM.
∴MF=GE,DF=MG,∠AFM+∠AFD=∠AGM+∠AGE,
∴∠DFM=∠MGE.
在△DFM和△MGE中,
,
∴△DFM≌△MGE(SAS),
∴DM=ME;
(3)如图2,取BC、AB和AC的中点M、F、G,连接MF、DF、MG、EG.

∴MF∥AC,MF=
AC,MG∥AB,MG=
AB,
∴四边形MFAG是平行四边形,
∴MG=AF,MF=AG,∠AFM=∠AGM,
∵△ADB和△AEC是等腰直角三角形,
∴DF=AF,GE=AG,∠AFD=∠BFD=∠AGE=90°,
∴MF=EG,DF=MG,∠AFM-∠AFD=∠AGM-∠AGE,
即∠DFM=∠MGE.
在△DFM和△MGE中,
,
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
MF=GE ∠DFM=∠MGE DF=MG MF=GE MF=GE MF=GE∠DFM=∠MGE ∠DFM=∠MGE ∠DFM=∠MGEDF=MG DF=MG DF=MG
∴△DFM≌△MGE(SAS),
∴DM=ME;
(3)如图2,取BC、AB和AC的中点M、F、G,连接MF、DF、MG、EG.

∴MF∥AC,MF=
AC,MG∥AB,MG=
AB,
∴四边形MFAG是平行四边形,
∴MG=AF,MF=AG,∠AFM=∠AGM,
∵△ADB和△AEC是等腰直角三角形,
∴DF=AF,GE=AG,∠AFD=∠BFD=∠AGE=90°,
∴MF=EG,DF=MG,∠AFM-∠AFD=∠AGM-∠AGE,
即∠DFM=∠MGE.
在△DFM和△MGE中,
,
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
1 2 1 1 12 2 2AC,MG∥AB,MG=
AB,
∴四边形MFAG是平行四边形,
∴MG=AF,MF=AG,∠AFM=∠AGM,
∵△ADB和△AEC是等腰直角三角形,
∴DF=AF,GE=AG,∠AFD=∠BFD=∠AGE=90°,
∴MF=EG,DF=MG,∠AFM-∠AFD=∠AGM-∠AGE,
即∠DFM=∠MGE.
在△DFM和△MGE中,
,
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
1 2 1 1 12 2 2AB,
∴四边形MFAG是平行四边形,
∴MG=AF,MF=AG,∠AFM=∠AGM,
∵△ADB和△AEC是等腰直角三角形,
∴DF=AF,GE=AG,∠AFD=∠BFD=∠AGE=90°,
∴MF=EG,DF=MG,∠AFM-∠AFD=∠AGM-∠AGE,
即∠DFM=∠MGE.
在△DFM和△MGE中,
,
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
MF=EG ∠DFM=∠MGE DF=MG MF=EG MF=EG MF=EG∠DFM=∠MGE ∠DFM=∠MGE ∠DFM=∠MGEDF=MG DF=MG DF=MG
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
∵AB=AC,BM=CM,
∴AM⊥BC,
∴∠AMB=∠AMC=90°,
∵∠ADB=90°,
∴四边形ADBM四点共圆,
∴∠AMD=∠ABD=45°.
∵AM是对称轴,
∴∠AME=∠AMD=45°,
∴∠DME=90°,
∴MD⊥ME,故④正确,
故答案为:①②③④.
(2)MD=ME,
理由:如图1,取AB、AC的中点F、G,连接DF,MF,EG,MG,

∴AF=
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABD和△AEC是等腰直角三角形,
∴DF⊥AB,DF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AFD=∠AGE=90°,DF=AF,GE=AG.
∵M是BC的中点,
∴MF∥AC,MG∥AB,
∴四边形AFMG是平行四边形,
∴AG=MF,MG=AF,∠AFM=∠AGM.
∴MF=GE,DF=MG,∠AFM+∠AFD=∠AGM+∠AGE,
∴∠DFM=∠MGE.
在△DFM和△MGE中,
|
∴△DFM≌△MGE(SAS),
∴DM=ME;
(3)如图2,取BC、AB和AC的中点M、F、G,连接MF、DF、MG、EG.

∴MF∥AC,MF=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形MFAG是平行四边形,
∴MG=AF,MF=AG,∠AFM=∠AGM,
∵△ADB和△AEC是等腰直角三角形,
∴DF=AF,GE=AG,∠AFD=∠BFD=∠AGE=90°,
∴MF=EG,DF=MG,∠AFM-∠AFD=∠AGM-∠AGE,
即∠DFM=∠MGE.
在△DFM和△MGE中,
|
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABD和△AEC是等腰直角三角形,
∴DF⊥AB,DF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AFD=∠AGE=90°,DF=AF,GE=AG.
∵M是BC的中点,
∴MF∥AC,MG∥AB,
∴四边形AFMG是平行四边形,
∴AG=MF,MG=AF,∠AFM=∠AGM.
∴MF=GE,DF=MG,∠AFM+∠AFD=∠AGM+∠AGE,
∴∠DFM=∠MGE.
在△DFM和△MGE中,
|
∴△DFM≌△MGE(SAS),
∴DM=ME;
(3)如图2,取BC、AB和AC的中点M、F、G,连接MF、DF、MG、EG.

∴MF∥AC,MF=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形MFAG是平行四边形,
∴MG=AF,MF=AG,∠AFM=∠AGM,
∵△ADB和△AEC是等腰直角三角形,
∴DF=AF,GE=AG,∠AFD=∠BFD=∠AGE=90°,
∴MF=EG,DF=MG,∠AFM-∠AFD=∠AGM-∠AGE,
即∠DFM=∠MGE.
在△DFM和△MGE中,
|
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
| 1 |
| 2 |
∵△ABD和△AEC是等腰直角三角形,
∴DF⊥AB,DF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AFD=∠AGE=90°,DF=AF,GE=AG.
∵M是BC的中点,
∴MF∥AC,MG∥AB,
∴四边形AFMG是平行四边形,
∴AG=MF,MG=AF,∠AFM=∠AGM.
∴MF=GE,DF=MG,∠AFM+∠AFD=∠AGM+∠AGE,
∴∠DFM=∠MGE.
在△DFM和△MGE中,
|
∴△DFM≌△MGE(SAS),
∴DM=ME;
(3)如图2,取BC、AB和AC的中点M、F、G,连接MF、DF、MG、EG.

∴MF∥AC,MF=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形MFAG是平行四边形,
∴MG=AF,MF=AG,∠AFM=∠AGM,
∵△ADB和△AEC是等腰直角三角形,
∴DF=AF,GE=AG,∠AFD=∠BFD=∠AGE=90°,
∴MF=EG,DF=MG,∠AFM-∠AFD=∠AGM-∠AGE,
即∠DFM=∠MGE.
在△DFM和△MGE中,
|
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AFD=∠AGE=90°,DF=AF,GE=AG.
∵M是BC的中点,
∴MF∥AC,MG∥AB,
∴四边形AFMG是平行四边形,
∴AG=MF,MG=AF,∠AFM=∠AGM.
∴MF=GE,DF=MG,∠AFM+∠AFD=∠AGM+∠AGE,
∴∠DFM=∠MGE.
在△DFM和△MGE中,
|
∴△DFM≌△MGE(SAS),
∴DM=ME;
(3)如图2,取BC、AB和AC的中点M、F、G,连接MF、DF、MG、EG.

∴MF∥AC,MF=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形MFAG是平行四边形,
∴MG=AF,MF=AG,∠AFM=∠AGM,
∵△ADB和△AEC是等腰直角三角形,
∴DF=AF,GE=AG,∠AFD=∠BFD=∠AGE=90°,
∴MF=EG,DF=MG,∠AFM-∠AFD=∠AGM-∠AGE,
即∠DFM=∠MGE.
在△DFM和△MGE中,
|
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
| 1 |
| 2 |
∴∠AFD=∠AGE=90°,DF=AF,GE=AG.
∵M是BC的中点,
∴MF∥AC,MG∥AB,
∴四边形AFMG是平行四边形,
∴AG=MF,MG=AF,∠AFM=∠AGM.
∴MF=GE,DF=MG,∠AFM+∠AFD=∠AGM+∠AGE,
∴∠DFM=∠MGE.
在△DFM和△MGE中,
|
∴△DFM≌△MGE(SAS),
∴DM=ME;
(3)如图2,取BC、AB和AC的中点M、F、G,连接MF、DF、MG、EG.

∴MF∥AC,MF=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形MFAG是平行四边形,
∴MG=AF,MF=AG,∠AFM=∠AGM,
∵△ADB和△AEC是等腰直角三角形,
∴DF=AF,GE=AG,∠AFD=∠BFD=∠AGE=90°,
∴MF=EG,DF=MG,∠AFM-∠AFD=∠AGM-∠AGE,
即∠DFM=∠MGE.
在△DFM和△MGE中,
|
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
|
| MF=GE |
| ∠DFM=∠MGE |
| DF=MG |
| MF=GE |
| ∠DFM=∠MGE |
| DF=MG |
| MF=GE |
| ∠DFM=∠MGE |
| DF=MG |
| MF=GE |
| ∠DFM=∠MGE |
| DF=MG |
∴△DFM≌△MGE(SAS),
∴DM=ME;
(3)如图2,取BC、AB和AC的中点M、F、G,连接MF、DF、MG、EG.

∴MF∥AC,MF=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形MFAG是平行四边形,
∴MG=AF,MF=AG,∠AFM=∠AGM,
∵△ADB和△AEC是等腰直角三角形,
∴DF=AF,GE=AG,∠AFD=∠BFD=∠AGE=90°,
∴MF=EG,DF=MG,∠AFM-∠AFD=∠AGM-∠AGE,
即∠DFM=∠MGE.
在△DFM和△MGE中,
|
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形MFAG是平行四边形,
∴MG=AF,MF=AG,∠AFM=∠AGM,
∵△ADB和△AEC是等腰直角三角形,
∴DF=AF,GE=AG,∠AFD=∠BFD=∠AGE=90°,
∴MF=EG,DF=MG,∠AFM-∠AFD=∠AGM-∠AGE,
即∠DFM=∠MGE.
在△DFM和△MGE中,
|
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
| 1 |
| 2 |
∴四边形MFAG是平行四边形,
∴MG=AF,MF=AG,∠AFM=∠AGM,
∵△ADB和△AEC是等腰直角三角形,
∴DF=AF,GE=AG,∠AFD=∠BFD=∠AGE=90°,
∴MF=EG,DF=MG,∠AFM-∠AFD=∠AGM-∠AGE,
即∠DFM=∠MGE.
在△DFM和△MGE中,
|
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
|
| MF=EG |
| ∠DFM=∠MGE |
| DF=MG |
| MF=EG |
| ∠DFM=∠MGE |
| DF=MG |
| MF=EG |
| ∠DFM=∠MGE |
| DF=MG |
| MF=EG |
| ∠DFM=∠MGE |
| DF=MG |
∴△DFM≌△MGE(SAS),
∴MD=ME,∠MDF=∠EMG.
∵MG∥AB,
∴∠MHD=∠BFD=90°,
∴∠HMD+∠MDF=90°,
∴∠HMD+∠EMG=90°,
即∠DME=90°,
∴△DME为等腰直角三角形.
看了 某数学活动小组在作三角形的拓...的网友还看了以下:
已知四边形ABCD,A(2,1)B(-1,2)C(-2,-3)D(1,-2)求做四边形ABCD关于 2020-05-16 …
如图,两张等宽的纸条交叉重叠在一起,重叠的部分ABCD是菱形吗?求证:(1)四边形ABCD是平行四 2020-05-16 …
扇形OAB的圆心角为90°,四边形OCDE是边长为1的正方形如图,扇形AOB的圆心角为90°,四边 2020-05-17 …
关于与三角形有关的线段选择题1.在三角形ABC中,角C是钝角,若作BC边上的高线AD,则步骤应是( 2020-06-05 …
1261年,我国宋代数学家杨辉写了一本书《详解九章算术》.书中记载了一个用数字排成的三角形我们叫作 2020-06-13 …
如图是尿的形成示意图,请据图回答(1)在尿的形成过程中要经过两个作用过程,即图中的A作用和C作用. 2020-06-22 …
如图是尿的形成示意图,请据图回答问题:(1)图中结构G、H和I构成一个肾单位.(2)在尿的形成过程 2020-07-01 …
如图实心点的个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作a1=1,第2个五角 2020-07-09 …
如图是尿的形成示意图,请据图回答:(1)图中结构G、H和图中的C构成一个肾单位.(2)在尿的形成过程 2020-12-21 …
1.如何作一个面积为14平方厘米的正方形,最好连文带图的.2.已知:用长度为a、b、c的线段作三角形 2020-12-25 …